
【题目】如图,在正方形![]() 中,点
中,点![]() 是边
是边![]() 上的一点(不与
上的一点(不与![]() 、
、![]() 重合),点
重合),点![]() 在
在![]() 的延长线上,且满足
的延长线上,且满足![]() ,连接
,连接![]() 、
、![]() ,
,![]() 与边
与边![]() 交于点
交于点![]() .
.
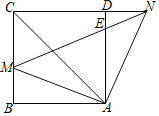
(1)求证:![]() ;
;
(2)如果![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)由正方形的性质得出AB=AD,∠CAD=∠ACB=45°,∠BAD=∠CDA=∠B=90°,然后根据等量代换得出∠BAM=∠DAN,利用ASA可证△ABM≌△ADN,从而利用全等三角形的性质即可证明AM=AN;
(2)根据正方形的性质和![]() 得出∠CAM=∠NAD,∠ACB=∠MNA=45°,从而有△AMC∽△AEN,则
得出∠CAM=∠NAD,∠ACB=∠MNA=45°,从而有△AMC∽△AEN,则![]() =
=![]() ,又因为AN=AM,所以有AN2=AEAC.
,又因为AN=AM,所以有AN2=AEAC.
解:证明(1)∵四边形ABCD是正方形,
∴AB=AD,∠CAD=∠ACB=45°,∠BAD=∠CDA=∠B=90°,
∴∠BAM+∠MAD=90°,∠ADN=90°
∵∠MAN=90°,
∴∠MAD+∠DAN=90°,
∴∠BAM=∠DAN,
且AD=AB,∠ABC=∠ADN=90°
∴△ABM≌△ADN(ASA)
∴AM=AN,
(2)∵AM=AN,∠MAN=90°,
∴∠MNA=45°,
∵∠CAD=2∠NAD=45°,
∴∠NAD=22.5°
∴∠CAM=∠MAN﹣∠CAD﹣∠NAD=22.5°
∴∠CAM=∠NAD,∠ACB=∠MNA=45°,
∴△AMC∽△AEN
∴![]() =
=![]() ,且AN=AM,
,且AN=AM,
∴AN2=AEAC


科目:初中数学 来源: 题型:
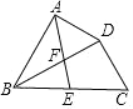
【题目】如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级10个班师生举行传统诗词进校园文艺表演,每班2个节目,有诗词吟诵与诗词吟唱两类节目,学校统计后发现诗词吟诵类节目比诗词吟唱类节目数的2倍少4个
(1)九年级师生表演的诗词吟诵与诗词吟唱类节目数各有多少个?
(2)该校八年级学生有诗词编舞节目参与,在诗词吟诵、诗词吟唱、诗词编舞三类节目中,每个节目的演出用时分别是5分钟,6分钟,8分钟,预计所有演出节目交接用时共花16分钟.若从14:30开始,17:00之前演出结束,问参与的诗词编舞类节目最多能有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
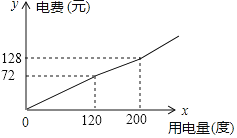
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
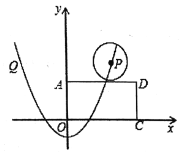
【题目】如图,平面坐标内,矩形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() 的半径为1,当圆心
的半径为1,当圆心![]() 在抛物线上从点
在抛物线上从点![]() 运动到点
运动到点![]() ,则在整个运动过程中,
,则在整个运动过程中,![]() 与矩形
与矩形![]() 只有一个公共点的情况共出现______次.
只有一个公共点的情况共出现______次.
查看答案和解析>>
科目:初中数学 来源: 题型:
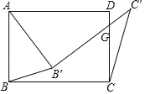
【题目】如图,在矩形ABCD中,将∠ABC绕点A按逆时针方向旋转一定角度后,BC的对应边B'C'交CD边于点G.连接BB'、CC',若AD=7,CG=4,AB'=B'G,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
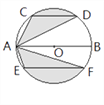
【题目】运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,它们的速度均为
匀速运动,它们的速度均为![]() .作
.作![]() 于
于![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() (
(![]() ),解答下列问题:
),解答下列问题:
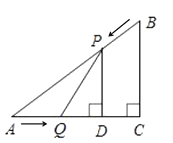
(1)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最大值;
的最大值;
(2)当![]() 的值为________________时,
的值为________________时,![]() 是等腰三角形
是等腰三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com