
 ,
, ,
, ,求该抛物线与
,求该抛物线与 轴公共点的坐标;
轴公共点的坐标; ,且当
,且当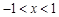 时,抛物线与
时,抛物线与 轴有且只有一个公共点,求
轴有且只有一个公共点,求 的取值范围;
的取值范围; ,且
,且 时,对应的
时,对应的 ;
; 时,对应的
时,对应的 ,试判断当
,试判断当 时,抛物线与
时,抛物线与 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
轴是否有公共点?若有,请证明你的结论;若没有,阐述理由. 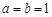 ,
, 时,抛物线为
时,抛物线为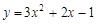
 的两个根为
的两个根为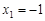 ,
, .
.  轴公共点的坐标是
轴公共点的坐标是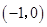 和
和 . ············· 2分
. ············· 2分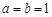 时,抛物线为
时,抛物线为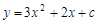 ,且与
,且与 轴有公共点.
轴有公共点. ,判别式
,判别式 ≥0,有
≥0,有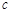 ≤
≤ . ·········· 3分
. ·········· 3分 时,由方程
时,由方程 ,解得
,解得 .
. 与
与 轴只有一个公共点
轴只有一个公共点 .········· 4分
.········· 4分 时,
时, 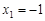 时,
时, ,
,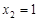 时,
时, .
. 时,该抛物线与
时,该抛物线与 轴有且只有一个公共点,考虑其对称轴为
轴有且只有一个公共点,考虑其对称轴为 ,
, 即
即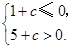
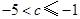 .
. 或
或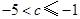 . ······················· 6分
. ······················· 6分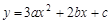 ,
, 时,
时,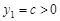 ;
;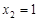 时,
时, ,
,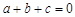 ,∴
,∴ .
. .而
.而 ,∴
,∴ ,即
,即 .
. . ······························· 7分
. ······························· 7分 的一元二次方程
的一元二次方程 的判别式
的判别式 ,
, 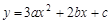 与
与 轴有两个公共点,顶点在
轴有两个公共点,顶点在 轴下方.········ 8分
轴下方.········ 8分 ,
,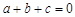 ,
, ,
, ,
, ,
, .
. 时,
时, ;
;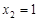 时,
时, ,观察图象,
,观察图象,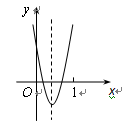
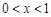 范围内,该抛物线与
范围内,该抛物线与 轴有两个公共点. ············ 11分解析:
轴有两个公共点. ············ 11分解析: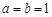 ,
, ,求出抛物线的解析式,从而求得与
,求出抛物线的解析式,从而求得与 轴公共点的坐标
轴公共点的坐标 时和当
时和当 时分别进行分析,求
时分别进行分析,求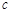 的取值范围
的取值范围 的一元二次方程
的一元二次方程 的判别式,确定抛物线与
的判别式,确定抛物线与 轴有两个公共点,顶点在
轴有两个公共点,顶点在 轴下方
轴下方 

科目:初中数学 来源:2012届福建省厦门市翔安区九年级适应性考试数学卷(带解析) 题型:填空题
已知抛物线 ,
,
(1)若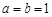 ,
,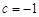 ,求该抛物线与
,求该抛物线与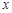 轴公共点的坐标;
轴公共点的坐标;
(2)若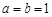 ,且当
,且当 时,抛物线与
时,抛物线与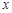 轴有且只有一个公共点,求
轴有且只有一个公共点,求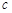 的取值范围;
的取值范围;
(3)若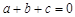 ,且
,且 时,对应的
时,对应的 ;
;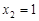 时,对应的
时,对应的 ,试判断当
,试判断当 时,抛物线与
时,抛物线与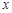 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线,
(1)若,
,求该抛物线与
轴公共点的坐标;
(2)若![]() ,且当
,且当![]() 时,抛物线与
时,抛物线与轴有且只有一个公共点,求
的取值范围;
(3)若,且
时,对应的
;
时,对应的
,试判断当
时,抛物线与
轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
【解析】(1)通过,
,求出抛物线的解析式,从而求得与
![]() 轴公共点的坐标
轴公共点的坐标
(2)从当时和当
时分别进行分析,求
![]() 的取值范围
的取值范围
(3)通过关于的一元二次方程
的判别式,确定抛物线与
轴有两个公共点,顶点在
轴下方
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线![]() ,
,
(1)若![]() ,且当
,且当![]() 时,抛物线与
时,抛物线与![]() 轴有且只有一个公共点,求
轴有且只有一个公共点,求![]() 的取值范围;
的取值范围;
(2)若![]() ,且当x=0时,对应的y>0;当x=1时,对应的y>0,试判断当
,且当x=0时,对应的y>0;当x=1时,对应的y>0,试判断当![]() 时,抛物线与
时,抛物线与![]() 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建省厦门市翔安区九年级适应性考试数学卷(解析版) 题型:填空题
已知抛物线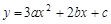 ,
,
(1)若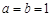 ,
,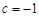 ,求该抛物线与
,求该抛物线与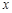 轴公共点的坐标;
轴公共点的坐标;
(2)若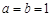 ,且当
,且当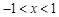 时,抛物线与
时,抛物线与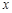 轴有且只有一个公共点,求
轴有且只有一个公共点,求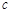 的取值范围;
的取值范围;
(3)若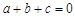 ,且
,且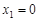 时,对应的
时,对应的 ;
;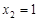 时,对应的
时,对应的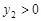 ,试判断当
,试判断当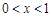 时,抛物线与
时,抛物线与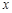 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
【解析】(1)通过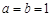 ,
,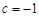 ,求出抛物线的解析式,从而求得与
,求出抛物线的解析式,从而求得与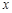 轴公共点的坐标
轴公共点的坐标
(2)从当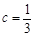 时和当
时和当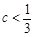 时分别进行分析,求
时分别进行分析,求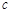 的取值范围
的取值范围
(3)通过关于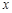 的一元二次方程
的一元二次方程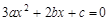 的判别式,确定抛物线与
的判别式,确定抛物线与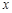 轴有两个公共点,顶点在
轴有两个公共点,顶点在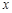 轴下方
轴下方
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com