【题目】为了应对全球新冠肺炎，满足抗疫物资的需求，某电机公司转型生产
呼吸机和
呼吸机，每台呼吸机比每台呼吸机的生产成本多200元，用5万元生产呼吸机与用4.5万元生产呼吸机的数量相等
（1）求每台呼吸机、呼吸机的生产成本各是多少元?
（2）该公司计划生产这两种呼吸机共50台进行试销，其中呼吸机为
台，生产总费用不超过9.8万元，试销时呼吸机每台售价2500元，呼吸机每台售价2180元，公司决定从销售呼吸机的利润中按每台捐献
元作为公司捐献国家抗疫的资金，若公司售完50台呼吸机并捐献资金后获得的利润不超过23000元，求
的取值范围．
【答案】（1）每台
呼吸机、
呼吸机的生产成本分别是2000元、1800元；（2）
【解析】
（1）设每台呼吸机的生产成本是
元，则每台呼吸机的生产成本是
元，根据数量=总价÷单价结合用5万元生产呼吸机与用4.5万元生产呼吸机的数量相等，即可得出关于x的分式方程，解之经检验后即可得出结论；
（2）根据题意可以求得x的取值范围和利润与x的函数关系式，然后根据一次函数的性质即可解答本题．
（1）设每台呼吸机的生产成本是元，则每台呼吸机的生产成本是元，根据题意得：
解之得，
经检验，是原分式方程的解．
答：每台呼吸机、呼吸机的生产成本分别是2000元、1800元
（2）根据题意得：
，
解得：
，
设公司售完50台呼吸机并捐献资金后获得的利润为
元，
则
，
，
，随
的增大而增大，
∴当
时，取得最大值，
，解得：
，
的取值范围是
科目：初中数学 来源： 题型：
【题目】如图，在等边
和等边
中，过
作
交
延长线于点
．
（1）如图，求证：四边形
为菱形；
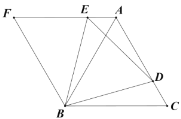
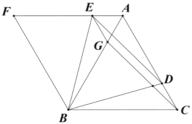
（2）如图，过
作
交
于点
，连接
，不添加任何辅助线，直接写出与
相等的所有角（不包括）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在网格纸中，
、
都是格点，以为圆心，
为半径作圆，用无刻度的直尺完成以下画图：（不写画法）
（1）在圆①中画圆的一个内接正六边形
；
（2）在图②中画圆的一个内接正八边形
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AC，BD为四边形ABCD的对角线，AC⊥BC，AB⊥AD，CA＝CD．若tan∠BAC＝
．则tan∠DBC的值是（ ）
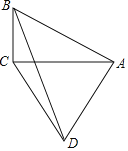
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，抛物线
与
轴交于点A，将点A向右平移2个单位长度，得到点B，点B在抛物线上．
（1）求点B的坐标（用含
的式子表示）；
（2）求抛物线的对称轴；
（3）已知点
，
．若抛物线与线段PQ恰有一个公共点，结合函数图象，求的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
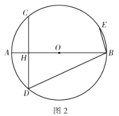
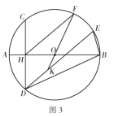
【题目】在
中，
为直径，CD与相较于点H，弧AC=弧AD
（1）如图1，求证：
;
（2）如图2，弧BC上有一点E，若弧CD=弧CE，求证：
;
（3）如图3，在（2）的条件下，点F在上，连接
，延长FO交
于点K，若
，求．
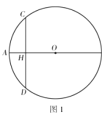
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了了解2018年北京市乘坐地铁的每个人的月均花费情况，相关部门随机调查了1000人乘坐地铁的月均花费(单位：元)，绘制了如下频数分布直方图.根据图中信息，下面3个推断中，合理的是______.
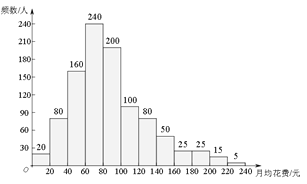
①小明乘坐地铁的月均花费是75元，那么在所调查的1000人中至少有一半的人月均花费超过小明；
②估计平均每人乘坐地铁的月均花费的范围是60～120元；
③如果规定消费达到一定数额可以享受折扣优惠，并且享受折扣优惠的人数控制在20%左右，那么乘坐地铁的月均花费达到120元的人可享受折扣.
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目：初中数学 来源： 题型：
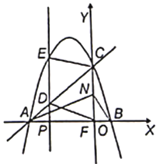
【题目】如图，抛物线
与坐标轴分别交于点
、
，其中有
，
，过抛物线对称轴左侧的一点
做
轴于点
，点
在
上运动，点
是
上的动点，
连接
，
．
（1）求抛物线的解析式及点的坐标；
（2）求
的最小值；
（3）点
是对称轴的左侧抛物线上的一个点，当
时，求点的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
