
【题目】如图,在网格纸中,![]() 、
、![]() 都是格点,以
都是格点,以![]() 为圆心,
为圆心,![]() 为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
(1)在圆①中画圆![]() 的一个内接正六边形
的一个内接正六边形![]() ;
;
(2)在图②中画圆![]() 的一个内接正八边形
的一个内接正八边形![]() .
.

【答案】(1)见解析;(2)见解析
【解析】
(1)设AO的延长线与圆交于点D,根据正六边形的性质,点D即为正六边形的一个顶点,且正六边形的边长等于圆的半径,根据垂直平分线的性质即可确定其它的顶点;
(2)先求出内接八边形的中心角,然后根据正方形的性质即可找到各个顶点.
(1)设AO的延长线与圆交于点D,
根据圆的内接正六边形的性质,点D即为正六边形的一个顶点,且正六边形的边长等于圆的半径,即OB=AB,故在图中找到AO的中垂线与圆的交点即为正六边形的顶点B和F;同理:在图中找到OD的中垂线与圆的交点即为正六边形的顶点C和E,连接AB、BC、CD、DE、EF、FA,如图①,正六边形![]() 即为所求.
即为所求.
(2)圆的内接八边形的中心角为360°÷8=45°,而正方形的对角线与边的夹角也为45°
∴在如②图所示的正方形OMNP中,连接对角线ON并延长,交圆于点B,此时∠AON=45°;∵∠NOP=45°,
∴OP的延长线与圆的交点即为点C
同理,即可确定点D、E、F、G、H的位置,顺次连接,
如图②,正八边形![]() 即为所求.
即为所求.



科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知抛物线![]() (a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知
(a<0)与x轴交于A、B两点(点A在点B左侧),与y轴负半轴交于点C,顶点为D,已知![]() :S四边形ACBD=1:4.
:S四边形ACBD=1:4.
(1)求点D的坐标(用仅含c的代数式表示);
(2)若tan∠ACB=![]() ,求抛物线的解析式.
,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
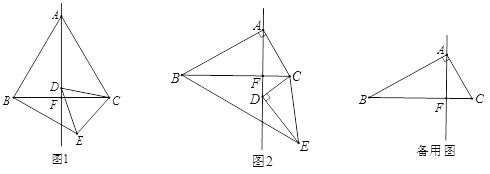
【题目】(1)问题发现:如图1,在△ABC中和△DCE中,![]() ,
,![]() ,
,![]() ,点D是BC的垂线AF上任意一点.填空:
,点D是BC的垂线AF上任意一点.填空:
①![]() 的值为 ;
的值为 ;
②∠ABE的度数为 .
(2)类比探究:如图2,在△ABC中和△DCE中,![]() ,
,![]() ,点D是BC的垂线AF上任意一点.请判断
,点D是BC的垂线AF上任意一点.请判断![]() 的值及∠ABE的度数,并说明理由;
的值及∠ABE的度数,并说明理由;
(3) 拓展延伸:在(2)的条件下,若![]() ,
,![]() ,请直接写出BE的长.
,请直接写出BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
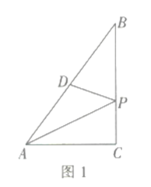
【题目】如图1,在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() .若
.若![]() 设
设 ![]() (当点
(当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值为
的值为![]() ),
),![]() .
.
小明根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.
![]() 通过取点、画图、计算,得到了
通过取点、画图、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
说明:补全表格时,相关数值保留一位小数.
(参考数据:![]() ) .
) .
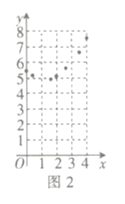
![]() 如图2,描出剩余的点,并用光滑的曲线画出该函数的图象.
如图2,描出剩余的点,并用光滑的曲线画出该函数的图象.
![]() 观察图象,下列结论正确的有 _ .
观察图象,下列结论正确的有 _ .
①函数有最小值,没有最大值
②函数有最小值,也有最大值
③当![]() 时,
时,![]() 随着
随着![]() 的增大而增大
的增大而增大
④当![]() 时,
时,![]() 随着
随着![]() 的增大而减小
的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
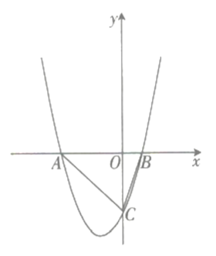
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 位于点
位于点![]() 的左侧),与
的左侧),与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
![]() 求点
求点![]() 的坐标.
的坐标.
![]() 若
若![]() 的面积为
的面积为![]() .
.
①求这条抛物线相应的函数解析式.
②在拋物线上是否存在一点![]() 使得
使得![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:⊙O的两条弦![]() ,
,![]() 相交于点
相交于点![]() ,且
,且![]() .
.
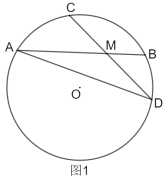
(1)如图1,连接![]() ,求证:
,求证:![]() .
.
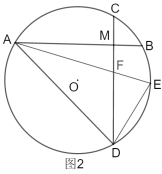
(2)如图2,在![]() ,在
,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
①判断![]() 与
与![]() 是否相等,并说明理由.
是否相等,并说明理由.
②若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了应对全球新冠肺炎,满足抗疫物资的需求,某电机公司转型生产![]() 呼吸机和
呼吸机和![]() 呼吸机,每台
呼吸机,每台![]() 呼吸机比每台
呼吸机比每台![]() 呼吸机的生产成本多200元,用5万元生产
呼吸机的生产成本多200元,用5万元生产![]() 呼吸机与用4.5万元生产
呼吸机与用4.5万元生产![]() 呼吸机的数量相等
呼吸机的数量相等
(1)求每台![]() 呼吸机、
呼吸机、![]() 呼吸机的生产成本各是多少元?
呼吸机的生产成本各是多少元?
(2)该公司计划生产这两种呼吸机共50台进行试销,其中![]() 呼吸机为
呼吸机为![]() 台,生产总费用不超过9.8万元,试销时
台,生产总费用不超过9.8万元,试销时![]() 呼吸机每台售价2500元,
呼吸机每台售价2500元,![]() 呼吸机每台售价2180元,公司决定从销售
呼吸机每台售价2180元,公司决定从销售![]() 呼吸机的利润中按每台捐献
呼吸机的利润中按每台捐献![]() 元作为公司捐献国家抗疫的资金,若公司售完50台呼吸机并捐献资金后获得的利润不超过23000元,求
元作为公司捐献国家抗疫的资金,若公司售完50台呼吸机并捐献资金后获得的利润不超过23000元,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com