
【题目】定义:在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,当
,当![]() 时,
时,![]() 点坐标为
点坐标为![]() ;当
;当![]() 时,
时,![]() 点坐标为
点坐标为![]() ,则称点
,则称点![]() 为点
为点![]() 的
的![]() 分变换点(其中
分变换点(其中![]() 为常数).例如:
为常数).例如:![]() 的0分变换点坐标为
的0分变换点坐标为![]() .
.
(1)点![]() 的1分变换点坐标为 ;点
的1分变换点坐标为 ;点![]() 的1分变换点在反比例函数
的1分变换点在反比例函数![]() 图像上,则
图像上,则![]() ;若点
;若点![]() 的1分变换点直线
的1分变换点直线![]() 上,则
上,则![]() ;
;
(2)若点![]() 在二次函数
在二次函数![]() 的图像上,点
的图像上,点![]() 为点
为点![]() 的3分变换点.
的3分变换点.
①直写出点![]() 所在函数的解析式;
所在函数的解析式;
②求点![]() 所在函数的图像与直线
所在函数的图像与直线![]() 交点坐标;
交点坐标;
③当![]() 时,点
时,点![]() 所在函数的函数值
所在函数的函数值![]() ,直接写出
,直接写出![]() 的取值范围;
的取值范围;
(3)点![]() ,
,![]() ,若点
,若点![]() 在二次函数
在二次函数![]() 的图像上,点
的图像上,点![]() 为点
为点![]() 的
的![]() 分变换点.当点
分变换点.当点![]() 所在函数的图像与线段
所在函数的图像与线段![]() 有两个公共点时,直接写出
有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)(-5,-7),4,8;(2)①点Q所在函数的关系式为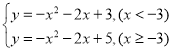 ;②交点坐标为(-4,-5)或(
;②交点坐标为(-4,-5)或(![]() ,-5);③t的取值范围为
,-5);③t的取值范围为![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据题意给的定义,即可得到答案;
(2)①设点Q的坐标为(a,b),分情况讨论,然后用a,b表示P的坐标,代入函数关系式整理变形即可;
②将y=-5代入函数关系式求解即可;
③先画出函数图像,结合函数图像找到相应的端点,求出端点坐标即可判断t的取值范围;
(3)先求出Q所在的函数关系式,再画出相应的函数图像分情况讨论,分别讨论当函数经过端点A、B及函数图像的顶点在线段AB上时的m的值,进而可得m的取值范围.
解:(1)∵5>1,
∴(5,7)的1分变换点为(-5,-7),
∵1≤1,
∴(1,6)的1分变换点为(-1,-4)
将(-1,-4)代入![]() ,得k=4,
,得k=4,
当a-1>1时,(a-1,5)的1分变换点为(1-a,-5)
将(1-a,-5)代入y=x+2得,-5=1-a+2,
解得a=8,
当a-1≤1时,(a-1,5)的1分变换点为(1-a,-3)
将(1-a,-3)代入y=x+2得,-3=1-a+2,
解得a=6,(舍去)
∴a=8,
故答案为:(-5,-7),4,8;
(2)①设点Q的坐标为(a,b)
当x>3时,若点P的3分变换点为Q(a,b),则a=-x,b=-y,
∴x=-a,y=-b,
将x=-a,y=-b代入![]()
得![]() ,
,
整理得:![]() ,
,
∴点Q所在函数的关系式为![]() (x<-3),
(x<-3),
当x≤3时,若点P的3分变换点为Q(a,b),则a=-x,b=-y+2,
∴x=-a,y=-b+2
将x=-a,y=-b+2代入![]()
得![]() ,
,
整理得:![]() ,
,
∴点Q所在函数的关系式为![]() (x≥-3),
(x≥-3),
综上所述,点Q所在函数的关系式为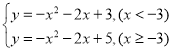
②将y=-5代入![]() 得
得![]()
解得:![]() (舍去)
(舍去)
将y=-5代入![]() 得
得![]()
解得:![]() (舍去)
(舍去)
综上所述,点![]() 所在函数的图像与直线
所在函数的图像与直线![]() 交点坐标为(-4,-5)或(
交点坐标为(-4,-5)或(![]() ,-5)
,-5)
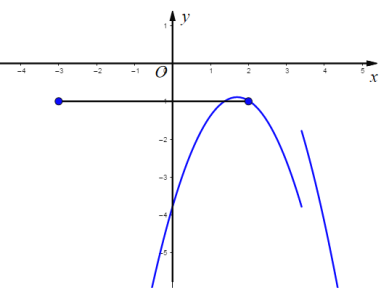
③如图,

由②可知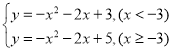 经过点(-4,-5)
经过点(-4,-5)
∵![]()
![]()
所以此抛物线的顶点坐标为(-1,6),
将x=-3代入![]() 得y=0,
得y=0,
将y=0代入![]() 得
得![]() (舍去)
(舍去)
∵当![]() 时,点
时,点![]() 所在函数的函数值
所在函数的函数值![]() ,
,
∴t的取值范围为![]() ;
;
(3)∵![]()
∴![]()
∵点![]() 在二次函数
在二次函数![]() 的图像上,
的图像上,
∴点Q在函数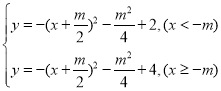 的图像上,
的图像上,
当m>0时,
如图,当![]() 经过点A(-3,-1)时
经过点A(-3,-1)时
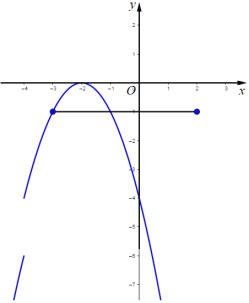
则![]()
解得![]() (舍去)
(舍去)
如图,当![]() 的顶点
的顶点![]() 在线段AB上时,
在线段AB上时,
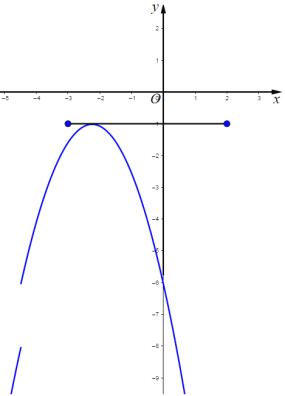
则![]() ,
,
解得![]() (舍去)
(舍去)
∴![]() ,
,
如图,当![]() 的端点落在线段AB上时,
的端点落在线段AB上时,
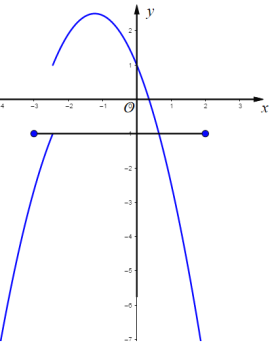
将![]() 代入
代入![]()
得![]()
解得:![]() (舍去)
(舍去)
如图,当![]() 经过点B(2,-1)时
经过点B(2,-1)时
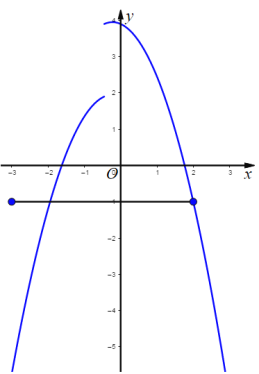
则![]()
解得:![]() (舍去)
(舍去)
∴![]() ,
,
如图,当![]() 经过点B(2,-1)时
经过点B(2,-1)时
则![]()
解得:![]() (舍去)
(舍去)
如图,当![]() 的顶点在线段AB上时,
的顶点在线段AB上时,
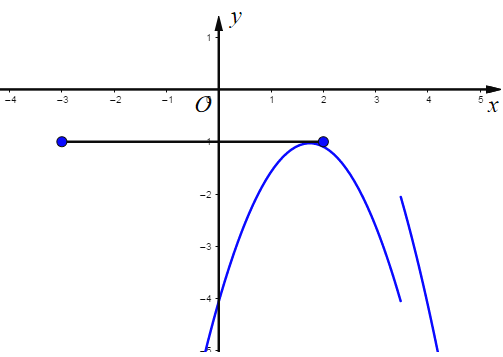
则![]()
解得:![]() (舍去)
(舍去)
∴![]() ,
,
综上所述,m的取值范围为:![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() =
=![]() (
(![]() 为任意实数)
为任意实数)
(1)无论![]() 取何值,抛物线
取何值,抛物线![]() 恒过两点________,________.
恒过两点________,________.
(2)当![]() 时,设抛物线
时,设抛物线![]() 在第一象限依次经过整数点(横、纵坐标均为整数的点)为
在第一象限依次经过整数点(横、纵坐标均为整数的点)为![]() ,
,![]() …
…![]() .将抛物线
.将抛物线![]() 沿直线
沿直线![]()
![]() 平移,平移后的抛物线记为
平移,平移后的抛物线记为![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() 的顶点为
的顶点为![]() (
(![]() ,例如
,例如![]() 时,抛物线
时,抛物线![]() 经过点
经过点![]() ,
,![]() 顶点为
顶点为![]() )
)
①抛物线![]() 的解析式为________;顶点坐标为________;
的解析式为________;顶点坐标为________;
②在抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标,并判断四边形
的坐标,并判断四边形![]() 的形状;若不存在,请说明理由.
的形状;若不存在,请说明理由.
③直接写出线段![]() 的长________.
的长________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
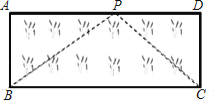
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格也相同).若购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元,购买
元,购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元.
元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需从体育用品商店一次性购买篮球和足球共![]() 个.要求购买总金额不能超过
个.要求购买总金额不能超过![]() 元,则最多能购买多少个篮球?
元,则最多能购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于世界人口增长、水污染以及水资源浪费等原因,全世界面临着淡水资源不足的问题,我国是世界上严重缺水的国家之一.节约用水是水资源合理利用的关键所在,是最快捷、最有效、最可行的维护水资源可持续利用的途径之一,为了调查居民的用水情况,有关部门对某小区的20户居民的月用水量进行了调查,数据如下(单位![]() ):
):
6.7 8.7 7.3 11.4 7.0 6.9 11.7 9.7 10.0 9.7
7.3 8.4 10.6 8.7 7.2 8.7 10.5 9.3 8.4 8.7
整理数据:按如下分段整理样本数据并补充表格(表1):
用水量 |
|
|
|
|
人数 |
| 6 | b | 4 |
分析数据:补全下列表格中的统计量(表2):
平均数 | 中位数 | 众数 |
8.85 |
| 8.7 |
得出结论:
(1)表中的![]() ,
,![]() ,
,![]() ;
;
(2)若用表1中的数据制作一个扇形统计图,![]() 所占的扇形圆心角的度数为 度;
所占的扇形圆心角的度数为 度;
(3)如果该小区有住户400户,根据样本估计用水量在![]() 的居民有多少户?
的居民有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是菱形,BC∥x轴,点B的坐标是(1,![]() ),坐标原点O是AB的中点.动圆⊙P的半径是
),坐标原点O是AB的中点.动圆⊙P的半径是![]() ,圆心在x轴上移动,若⊙P在运动过程中只与菱形ABCD的一边相切,则点P的横坐标m 的取值范围是_________.
,圆心在x轴上移动,若⊙P在运动过程中只与菱形ABCD的一边相切,则点P的横坐标m 的取值范围是_________.
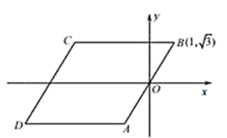
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为坐标原点,ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y=![]() (x>0)的图象经过点C且S△BEF=
(x>0)的图象经过点C且S△BEF=![]() ,则k的值为_____.
,则k的值为_____.
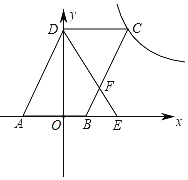
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市从一楼到二楼有一自动扶梯,如图是自动扶梯的侧面示意图,已知自动扶梯AB的坡度为1:2.4,AB的长度为13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处侧得C点的仰角为 42°,则二楼的层高BC约为(精确到0.1米,![]() ,
,![]() )( )
)( )
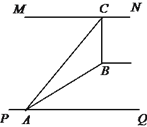
A.10.8米B.8.9米C.8.0米D.5.8米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com