
| 调往甲地(单位:吨) | 调往乙地(单位:吨) | |
| A | x | 13-x |
| B | 14-x | x-1 |
分析 (1)根据有理数的减法,可得A运往乙地的数量,根据甲地的需求量,有理数的减法,可得B运往乙地的数量,根据乙地的需求量,有理数的减法,可得B运往乙地的数量;
(2)根据A运往甲的费用加上A运往乙的费用,加上B运往甲的费用,加上B运往乙的费用,可得函数解析式;
(3)根据一次函数的性质,可得答案.
解答 解:(1)如下表: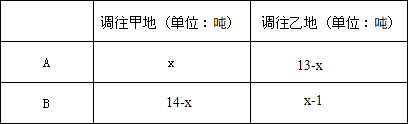
故答案为:13-x,14-x,x-1.
(2)根据题意得,W=50x+30(13-x)+60(14-x)+45(x-1)=5x+1185,
由$\left\{\begin{array}{l}{x≥0}\\{13-x≥0}\\{14-x≥0}\\{x-1≥0}\end{array}\right.$,
解得:1≤x≤13.
(3)在函数W=5x+1185中,k=5>0,
∴W随x的增大而增大,
当x=1时,W取得最小值,最小值为5×1+1185=1190.
此时A调往甲地1吨,调往乙地12吨,B调往甲地13吨.
点评 本题考查了一次函数的应用,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义,利用一次函数求最值时,关键是应用一次函数增减性.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:选择题
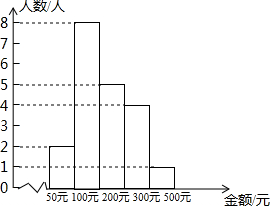 某企业为了解员工给灾区“爱心捐款”的情况,随机抽取部分员工的捐款金额整理绘制成如图所示的直方图,根据图中信息,下列结论正确的是( )
某企业为了解员工给灾区“爱心捐款”的情况,随机抽取部分员工的捐款金额整理绘制成如图所示的直方图,根据图中信息,下列结论正确的是( )| A. | 样本中位数是200元 | |
| B. | 样本容量是20 | |
| C. | 该企业员工捐款金额的极差是450元 | |
| D. | 该企业员工最大捐款金额是500元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
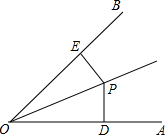 如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )
如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )| A. | 12 | B. | 18 | C. | 20 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
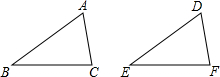 如图所示的△ABC和△DEF,给出下列三组条件:
如图所示的△ABC和△DEF,给出下列三组条件:| A. | 1组 | B. | 2组 | C. | 3组 | D. | 0组 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
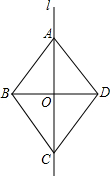 如图,直线l是四边形ABCD的对称轴,若AD∥BC,则下列结论:(1)AB∥CD;(2)AB=AD;(3)BO=CO,(4)BD平分∠ABC.其中正确的有(1)(2)(4)(填序号).
如图,直线l是四边形ABCD的对称轴,若AD∥BC,则下列结论:(1)AB∥CD;(2)AB=AD;(3)BO=CO,(4)BD平分∠ABC.其中正确的有(1)(2)(4)(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 不等式组的解集在数轴上表示出来如图所示,这个不等组为( )
不等式组的解集在数轴上表示出来如图所示,这个不等组为( )| A. | $\left\{\begin{array}{l}{x>-1}\\{x<3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x<-1}\\{x>3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x≥-1}\\{x≤3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x≥-1}\\{x<3}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com