
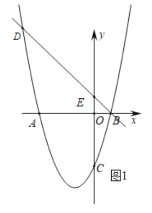
【题目】如图 1,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,点
,点![]() 和点
和点![]() ,并与直线
,并与直线![]() 交于另一点
交于另一点![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
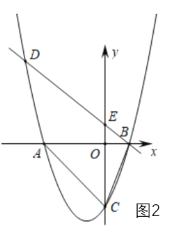
(2)如图 2,点![]() 为
为![]() 轴上一动点,连接
轴上一动点,连接![]() ,当
,当![]() 时,求点
时,求点 ![]() 的坐标;
的坐标;
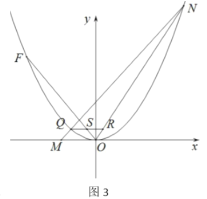
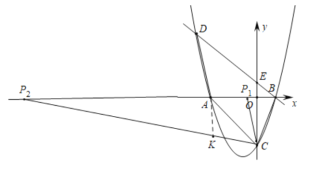
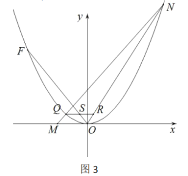
(3)如图 3,将抛物线![]() 平移,使其顶点是坐标原点
平移,使其顶点是坐标原点![]() ,得到抛物线
,得到抛物线![]() ;将直线
;将直线![]() 向下平移经过坐标原点
向下平移经过坐标原点![]() ,交抛物线
,交抛物线![]() 于另一点
于另一点![]() .点
.点![]() ,点
,点![]() 是
是![]() 上且位于 第一象限内一动点,
上且位于 第一象限内一动点,![]() 交
交![]() 于
于![]() 点,
点,![]() 轴分别交
轴分别交![]() 于
于![]() ,试说明:
,试说明:![]() 与
与![]() 存在一个确定的数量关系.
存在一个确定的数量关系.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,理由详见解析
,理由详见解析
【解析】
(1)利用待定系数法将A、B、C三点的坐标代入![]() 即可求解;
即可求解;
(2)P点分在A点的左边和右边的两种情况(图见详解),当P点在A点右边时,证出![]() ,即可通过相似比求出AP1的长度从而求出P1点坐标;当P点在A点左边时,通过证出
,即可通过相似比求出AP1的长度从而求出P1点坐标;当P点在A点左边时,通过证出![]() ,得到AK的长度,从而求出K点坐标,再利用待定系数法求出直线CK的解析式,P2就是直线CK与x轴的交点;
,得到AK的长度,从而求出K点坐标,再利用待定系数法求出直线CK的解析式,P2就是直线CK与x轴的交点;
(3)根据题意求出移动后的抛物线及直线OF的解析式,设出动点N的坐标,通过联立方程用N点的坐标表示出Q、R、S的横坐标,通过观察这三个横坐标的值即可得出数量关系.
解:(1)![]() 直线
直线![]() 经过B点,且B点在x轴上,
经过B点,且B点在x轴上,
![]() .
.
将![]() 代入
代入![]() ,得:
,得:
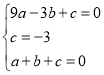
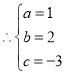
![]() 抛物线
抛物线![]() 的解析式
的解析式![]() .
.
(2)如下图所示,设![]()
由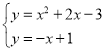
得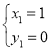 ,
,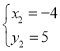
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
I.当点![]() 在点
在点![]() 的右边,记此时的点
的右边,记此时的点![]() 为
为![]() ,
,
![]() 时,
时,![]() .
.
![]()
![]()
![]()
![]()
![]()
II.当点![]() 在点
在点![]() 的左边,
的左边,![]() 时,
时,
记此时的点![]() 为
为![]() ,则有
,则有![]()
过点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]()
![]() 于点
于点![]() ,
,
则![]() ,又
,又![]() 公共边,
公共边,
![]() ,
,
![]()
![]()
![]() 设直线
设直线![]() ,
,![]() ,
,
![]() 直线
直线![]() ,
,
![]()
![]() 的坐标:
的坐标:![]() .
.
(3)![]() ,理由如下:
,理由如下:
依题意,抛物线![]() 的解析式:
的解析式:![]()
![]() 的解析式:
的解析式:![]()
![]()
设![]()
![]()
![]() 直线
直线![]() 的解析式:
的解析式:![]()
直线![]() 的解析式:
的解析式: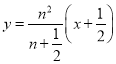
联立![]() 与
与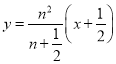
解得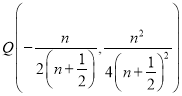
解得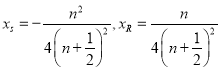
![]()
即点S是点Q、点R的中点,
即![]() .
.


科目:初中数学 来源: 题型:
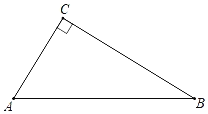
【题目】如图,在△ABC中,∠C=90°.
(1)用尺规作∠A的平分线交BC边于点D(不写作法,保留作图痕迹);
(2)在(1)的基础上,已知∠B=30°,AC=6,则线段AD的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】茶叶是安徽省主要经济作物之一,2020年新茶上市期间,某茶厂为获得最大利益,根据市场行情,把新茶价格定为400元/kg,并根据历年的相关数据整理出第x天(1≤x≤15,且x为整数)制茶成本(含采摘和加工)和制茶量的相关信息如下表.假定该茶厂每天制作和销售的新茶没有损失,且能在当天全部售出(当天收入=日销售额-日制茶成本)
制茶成本(元/kg) | 150+10x |
制茶量(kg) | 40+4x |
(1)求出该茶厂第10天的收入;
(2)设该茶厂第x天的收入为y(元).试求出y与x之间的函数关系式,并求出y的最大值及此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图(1),在等边三角形ABC中,点M是BC上的任意一点(不含端点B、C),连接AM,以AM为边作等边三角形AMN,连接CN,则∠ACN= °.
类比探究
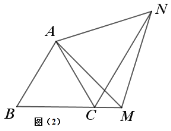
(2)如图(2),在等边三角形ABC中,点M是BC延长线上的任意一点(不含端点C),其他条件不变,(1)中的结论还成立吗?请说明理由.
拓展延伸
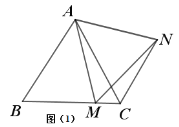
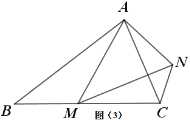
(3)如图(3),在等腰三角形ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连接AM,以AM为边作等腰三角形AMN,使AM=MN,连接CN.添加一个条件,使得∠ABC=∠ACN仍成立,写出你所添加的条件,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
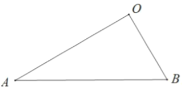
【题目】问题背景:如图 1,在![]() 和
和![]() 中,
中,![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .则
.则![]() 的值是____________.
的值是____________.
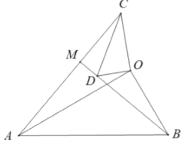
问题解决:如图 2,在问题背景的条件下,将![]() 绕点
绕点![]() 在平面内旋转,点
在平面内旋转,点![]() 始终在
始终在![]() 的外部,
的外部,![]() 所在直线交于点
所在直线交于点![]() ,若
,若![]() ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,![]() 的长是____________
的长是____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(![]() ,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤5a﹣2b<0;其中正确的个数有( )
,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤5a﹣2b<0;其中正确的个数有( )
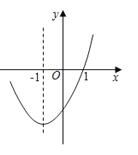
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
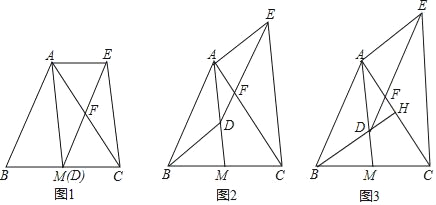
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM.
①求∠CAM的度数;
②当FH=![]() ,DM=4时,求DH的长.
,DM=4时,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
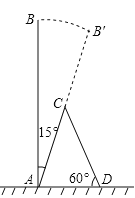
【题目】某次台风来袭时,一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断倒在地上,树的项部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求这棵大树AB原来的高度是( )米?(结果精确到个位,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈2.4)
≈2.4)
A.9B.10C.11D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )经过点A(
)经过点A(![]() ,
,![]() )和点B (
)和点B (![]() ,
,![]() ),且抛物线的对称轴在
),且抛物线的对称轴在![]() 轴的左侧. 下列结论: ①
轴的左侧. 下列结论: ① ![]() ; ② 方程
; ② 方程![]() 有两个不等的实数根; ③
有两个不等的实数根; ③![]() . 其中,正确结论的个数是( ).
. 其中,正确结论的个数是( ).
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com