
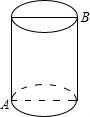
 如图,圆柱的高为12cm,底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离是多少cm?(π取3).
如图,圆柱的高为12cm,底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离是多少cm?(π取3).科目:初中数学 来源: 题型:
 (2007•西城区二模)如图,地上有一圆柱,在圆柱下底面的A点处有一蚂蚁,它想沿圆柱表面爬行.吃到上底面上与A点相对的B点处的食物(π的近似值取3,以下同).
(2007•西城区二模)如图,地上有一圆柱,在圆柱下底面的A点处有一蚂蚁,它想沿圆柱表面爬行.吃到上底面上与A点相对的B点处的食物(π的近似值取3,以下同).查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,有一个圆柱,它的高为12厘米,底面半径为3厘米,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面B点处的食物,则需要爬行的最短路程是
如图,有一个圆柱,它的高为12厘米,底面半径为3厘米,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面B点处的食物,则需要爬行的最短路程是查看答案和解析>>
科目:初中数学 来源:学习周报 数学 北师大八年级版 2009-2010学年 第1期 总第157期 北师大版 题型:022
1.如图,一个圆柱的底面周长是10 cm,圆柱的高为12 cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,沿圆柱侧面爬行的最短路程是________.
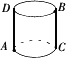
解:将圆柱沿侧面
AD剪开,得到如图所示的侧面展开图,求蚂蚁爬行的最短路程,就是求________的长.在Rt△ABC中,∠ACB=90°,AC=________,BC=________,由勾股定理,得AB2=AC2+BC2=________,所以AB=________,即蚂蚁爬行的最短路程是________.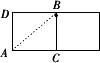
2.在上面求解过程中,用到的数学思想是________思想;在利用勾股定理解决实际问题时,除了这种数学思想,还会用到方程思想、分类思想等.在解决问题时要注意灵活运用这些数学思想哟!
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
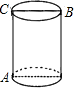 如图,地上有一圆柱,在圆柱下底面的A点处有一蚂蚁,它想沿圆柱表面爬行.吃到上底面上与A点相对的B点处的食物(π的近似值取3,以下同).
如图,地上有一圆柱,在圆柱下底面的A点处有一蚂蚁,它想沿圆柱表面爬行.吃到上底面上与A点相对的B点处的食物(π的近似值取3,以下同).查看答案和解析>>
科目:初中数学 来源:2007年北京市西城区中考数学二模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com