(1)解:由题意,得x
1•x
2=2b-1.
∵OA•OB=3,OA=x
1OB=x
2,
∴x
1•x
2=3.
∴2b-1=3.
∴b=2.
∴所求的抛物线解析式是:y=-x
2+4x-3.
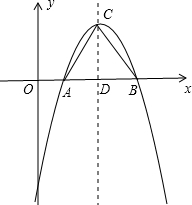
(2)证明:如图,
∵y=-x
2+4x-3=-(x-2)
2+1,
∴顶点C(2,1),D(2,0),CD=1.
令y=0,得-x
2+4x-3=0.
解得x
1=1,x
2=3.
∴A(1,0),B(3,0),AD=DB=1.
∴AD=DC=DB.
∴D为△ABC的外心.
(3)解法一:设抛物线存在点P(x,y),使S
△ABP=1.
由(2)可求得AB=3-1=2.
∴S
△ABP=

AB•|y|=

×2•|y|=1.
∴y=±1.
当y=1时,-x
2+4x-3=1,解得x
1=x
2=2.
当y=-1时,-x
2+4x-3=-1,解得x=2±

.
∴存在点P,使S
△ABP=1.
点P的坐标是(2,1)或(2+

,-1)或
(2-

,-1).
解法二:由(2)得S
△ABC=

AB•CD=

×2×1=1.
∴顶点C(2,1)是符合题意的一个点.
另一方面,直线y=-1上任一点M,能使S
△AMB=1,
把直线y=-1代入抛物线解析式,得-x
2+4x-3=-1.
解得x=2±

.
∴存在点P,使S
△ABP=1.
点P的坐标是(2,1)或(2+

,-1)或(2-

,-1).
分析:(1)∵OA•OB=3,即x
1•x
2=3,由根与系数关系可求b,确定抛物线解析式;
(2)根据抛物线的对称性可得DA=DB,只要证明AD=CD即可,求出抛物线的顶点C坐标和两交点A、B坐标即可解答本题;
(3)由于AB=2,∴△ABC的AB边上高是1,可知P点纵坐标为1或者-1,分别代入抛物线解析式,可求P点横坐标.
点评:本题考查了用根与系数关系求二次函数解析式,三角形外心的判断方法及三角形面积问题,具有较强的综合性.

 )两点,设OA•OB=3(O为坐标系原点).
)两点,设OA•OB=3(O为坐标系原点).
 AB•|y|=
AB•|y|= ×2•|y|=1.
×2•|y|=1. .
. ,-1)或
,-1)或 ,-1).
,-1). AB•CD=
AB•CD= ×2×1=1.
×2×1=1. .
. ,-1)或(2-
,-1)或(2- ,-1).
,-1).

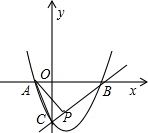 A是抛物线与x轴的另一个交点.
A是抛物线与x轴的另一个交点.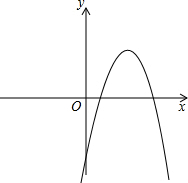 已知一元二次方程-x2+bx+c=0的两个实数根是m,4,其中0<m<4.
已知一元二次方程-x2+bx+c=0的两个实数根是m,4,其中0<m<4.