
【题目】已知直线y1=x﹣5与双曲线y2=﹣![]() .
.
(1)求证:无论p取何值时,两个函数的图象恒有两个交点;
(2)设两个交点分别为A(x1,y1)、B(x2,y2),且满足x12+x22=3x1x2,求实数p的值.
【答案】(1)证明见解析;(2)p=±1
【解析】
(1)根据两个函数解析式,得到方程x2﹣5x+6﹣p2=0,求根的判别式△,当△>0时,方程总有两个不相等的实数根;
(2)根据根与系的关系求出两根和与两根积,再把x12+x22=3x1x2变形,化成和与乘积的形式,代入计算,得到一个关于p的一元二次方程,解方程即可.
解:(1)联立方程组 ,
,
可得x2﹣5x+6﹣p2=0,
∴△=(﹣5)2﹣4×1×(6﹣p2)=25﹣24+4p2=1+4p2,
∵无论p取何值时,总有4p2≥0,
∴△=1+4p2>0,
∴无论p取何值时,方程总有两个不相等的实数根;
(2)∵x1+x2=5,x1x2=6﹣p2,
又∵x12+x22=3x1x2,
∴(x1+x2)2﹣2x1x2=3x1x2,
∴52=5(6﹣p2),
解得p=±1,
∴实数p的值为±1.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2,当a≤x≤b时m≤y≤n,则下列说法正确的是( )
A.当n﹣m=1时,b﹣a有最小值
B.当n﹣m=1时,b﹣a有最大值
C.当b﹣a=1时,n﹣m无最小值
D.当b﹣a=1时,n﹣m有最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年“众志成城,抗击肺炎”,郑州
年“众志成城,抗击肺炎”,郑州![]() 会展中心“大玉米”以灯光字幕给武汉加油,已知一安全巡视员站在如意湖湖边
会展中心“大玉米”以灯光字幕给武汉加油,已知一安全巡视员站在如意湖湖边![]() 处观看,测得“武”字低端
处观看,测得“武”字低端![]() 的仰角为
的仰角为![]() ,当巡视员沿着坡面
,当巡视员沿着坡面![]() 向上走到
向上走到![]() 处,此时测得“武”字顶端
处,此时测得“武”字顶端![]() 的仰角为
的仰角为![]() .已知坡面
.已知坡面![]() 的坡度为
的坡度为![]() ,
,![]() ,
,![]() .
.

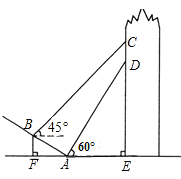
(1)求点![]() 到水平面
到水平面![]() 的距离
的距离![]() ;
;
(2)求“武”字的高度![]() .
.
(结果精确到![]() .参考数据:
.参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过
经过![]() ,
,![]() 两点.
两点.
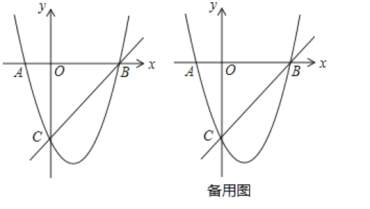
(1)求抛物线的解析式;
(2)过点![]() 作直线
作直线![]() 轴交抛物线于另一点
轴交抛物线于另一点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的一个动点,且在抛物线对称轴的右侧,过点
下方抛物线上的一个动点,且在抛物线对称轴的右侧,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数解析式(不要求写出自变量
之间的函数解析式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() (点
(点![]() 在线段
在线段![]() 上),
上),![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求线段
时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知半径为2的⊙O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4),则PDCD的最大值是( ).
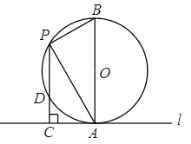
A.2B.3C.4D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】CBA球赛已经开始,某体育用品商店预测某球队的球服能够畅销,就用![]() 万元购入了一批球服,上市后很快就脱销,该商店又用
万元购入了一批球服,上市后很快就脱销,该商店又用![]() 万元购入第二批该球队的球服,所购数量是第一批购入数量的2倍,但每套进价多了10 元.如果该商店购入的两批球服售价一样,且要求两批球服全部售完后总利润率不低于
万元购入第二批该球队的球服,所购数量是第一批购入数量的2倍,但每套进价多了10 元.如果该商店购入的两批球服售价一样,且要求两批球服全部售完后总利润率不低于![]() ,那么每套球服的售价至少是( )元.(利润率
,那么每套球服的售价至少是( )元.(利润率![]() 利润
利润![]() 成本
成本![]() )
)
A.160B.180C.200D.220
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图所示,在直角坐标系中,以![]() 为圆心的
为圆心的![]() 与
与![]() 轴相交于
轴相交于![]() 两点,与
两点,与![]() 轴相交于
轴相交于![]() 两点,连接
两点,连接![]() .
.
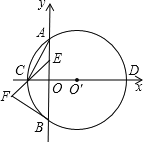
(1)![]() 上有一点
上有一点![]() ,使得
,使得![]() .求证
.求证![]() ;
;
(2)在(1)的结论下,延长![]() 到
到![]() 点,连接
点,连接![]() ,若
,若![]() ,请证明
,请证明![]() 与
与![]() 相切;
相切;
(3)如果![]() ,
,![]() 的半径为2,求(2)中直线
的半径为2,求(2)中直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
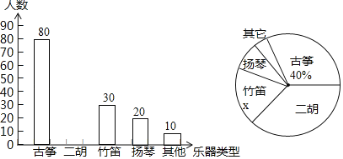
【题目】某校为了了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱的乐器),现将收集到的数据绘制成如下两幅不完整的统计图.
(1)这次共抽取 学生调查,扇形统计图中的x= ;
(2)请补全统计图;
(3)在扇形统计图中“扬琴”所对扇形的圆心角是多少度;
(4)若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
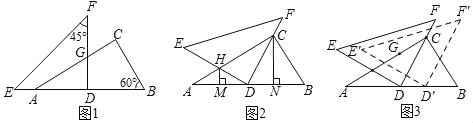
【题目】将一副三角尺按图1摆放,等腰直角三角尺的直角边DF恰好垂直平分AB,与AC相交于点G,![]() .
.
(1)求GC的长;
(2)如图2,将△DEF绕点D顺时针旋转,使直角边DF经过点C,另一直角边DE与AC相交于点H,分别过H、C作AB的垂线,垂足分别为M、N,通过观察,猜想MD与ND的数量关系,并验证你的猜想.
(3)在(2)的条件下,将△DEF沿DB方向平移得到△D′E′F′,当D′E′恰好经过(1)中的点G时,请直接写出DD′的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com