
【题目】问题背景
如图![]() ,在正方形
,在正方形![]() 的内部,作
的内部,作![]() ,根据三角形全等的条件,易得
,根据三角形全等的条件,易得![]() ≌
≌![]() ≌
≌![]() ≌
≌![]() ,从而得到四边形
,从而得到四边形![]() 是正方形.
是正方形.
类比探究
如图![]() ,在正
,在正![]() 的内部,作
的内部,作![]() ,
, ![]() ,
, ![]() ,
, ![]() 两两相交于
两两相交于![]() ,
, ![]() ,
, ![]() 三点(
三点(![]() ,
, ![]() ,
, ![]() 三点不重合).
三点不重合).
(![]() )
)![]() ,
, ![]() ,
, ![]() 是否全等?如果是,请选择其中一对进行证明.
是否全等?如果是,请选择其中一对进行证明.
(![]() )
)![]() 是否为正三角形?请说明理由.
是否为正三角形?请说明理由.
(![]() )进一步探究发现,图
)进一步探究发现,图![]() 中的
中的![]() 的三边存在一定的等量关系,设
的三边存在一定的等量关系,设![]() ,
, ![]() ,
, ![]() ,请探索
,请探索![]() ,
, ![]() ,
, ![]() 满足的等量关系.
满足的等量关系.

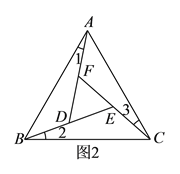

【答案】(1)见解析;(2)是;(3)![]()
【解析】试题分析:(1)由正三角形的性质得出∠CAB=∠ABC=∠BCA=60°,AB=BC,证出∠ABD=∠BCE,由ASA证明△ABD≌△BCE即可;
(2)由全等三角形的性质得出∠ADB=∠BEC=∠CFA,证出∠FDE=∠DEF=∠EFD,即可得出结论;
(3)作AG⊥BD于G,由正三角形的性质得出∠ADG=60°,在Rt△ADG中,DG=![]() b,AG=
b,AG=![]() b,在Rt△ABG中,由勾股定理即可得出结论.
b,在Rt△ABG中,由勾股定理即可得出结论.
试题解析:( ![]() )
)![]() ≌
≌![]() ≌
≌![]() ,理由如下:
,理由如下:
∵![]() 是正三角形,
是正三角形,
∴![]() ,
, ![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中, 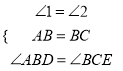 ,
,
∴![]() ≌
≌![]() ,
,
同理可得![]() ≌
≌![]() ,
,
∴![]() ≌
≌![]() ≌
≌![]() .
.
(![]() )
)![]() 是正三角形,理由如下.
是正三角形,理由如下.
∵![]() ≌
≌![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是正三角形.
是正三角形.
(![]() )作
)作![]() 于
于![]() ,如图所示:
,如图所示:
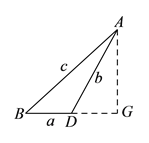
∵![]() 是正三角形,
是正三角形,
∴![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
在![]() 中,
中, 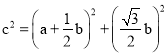
∴![]() .
.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于点
于点![]() .
.
(![]() )试证明:无论点
)试证明:无论点![]() 运动到
运动到![]() 上何处时,都有
上何处时,都有![]() ≌
≌![]() .
.
(![]() )若点
)若点![]() 从点
从点![]() 运动到点
运动到点![]() ,再继续在
,再继续在![]() 上运动到点
上运动到点![]() ,在整个运动过程中,点
,在整个运动过程中,点![]() 以每秒
以每秒![]() 单位长度的速度匀速运动,当
单位长度的速度匀速运动,当![]() 恰为等腰三角形,求点
恰为等腰三角形,求点![]() 运动的时间.
运动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在下列横线上用含有a,b的代数式表示相应图形的面积.

① ________;②________;③________;④________.
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示:_________________________;
(3)利用(2)的结论计算99992+2×9999×1+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象.下列说法错误的是( )
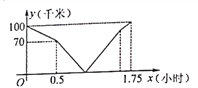
A. 乙先出发的时间为0.5小时 B. 甲的速度是80千米/小时
C. 甲出发0.75小时后两车相遇 D. 甲到B地比乙到A地迟5分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④0<CE≤6.4.其中正确的结论是______________.(填序号)
;④0<CE≤6.4.其中正确的结论是______________.(填序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
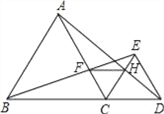
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F, AD交CE于H.
(1)求证:∠CAD=∠CBE
(2)求证:FH∥BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com