
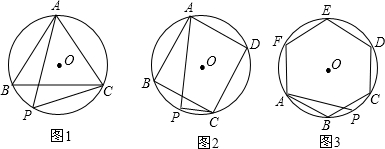
 如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC
如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC分析 (1)根据圆周角定理可得∠BOC=2∠BAC,∠AOB=2∠ACB,再根据条件∠AOB=2∠BOC可得∠ACB=2∠BAC;
(2)设∠BAC=x°,则∠OAB=2∠BAC=2x°,再表示出∠AOB=2∠ACB=4∠BAC=4x°,再根据三角形内角和为180°可得方程4x+2x+2x=180,再解即可得x的值,进而可得答案.
解答 (1)证明:在⊙O中,
∵∠AOB=2∠ACB,∠BOC=2∠BAC,
∵∠AOB=2∠BOC.
∴∠ACB=2∠BAC.
(2)解:设∠BAC=x°.
∵AC平分∠OAB,
∴∠OAB=2∠BAC=2x°,
∵∠AOB=2∠ACB,∠ACB=2∠BAC,
∴∠AOB=2∠ACB=4∠BAC=4x°,
在△OAB中,
∠AOB+∠OAB+∠OBA=180°,
∴4x+2x+2x=180,
解得:x=22.5,
∴∠AOC=6x°=135°.
点评 此题主要考查了圆周角定理,关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
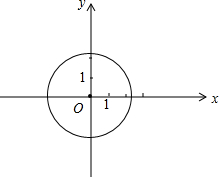 在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),若a=|x1-x2|,b=|y1-y2|,则记作(P,Q)→{a,b }.
在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),若a=|x1-x2|,b=|y1-y2|,则记作(P,Q)→{a,b }.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 日期 | 摘要 | 币种 | 存/取款金额 | 余额 | 操作员 | 备注 |
| 151101 | 北京水费 | RMB钞 | -125.45 | 874.55 | 010005B25 | 折 |
| 160101 | 北京水费 | RMB钞 | -136.02 | 738.53 | 010005Y03 | 折 |
| 160301 | 北京水费 | RMB钞 | -132.36 | 606.17 | 010005D05 | 折 |
| 160501 | 北京水费 | RMB钞 | -128.59 | 477.58 | 01000K19 | 折 |
| A. | 738.53元 | B. | 125.45元 | C. | 136.02元 | D. | 477.58元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com