
【题目】在平面直角坐标系中,点![]() ,
,![]() 为反比例函数
为反比例函数![]() 上的两个动点,以
上的两个动点,以![]() ,
,![]() 为顶点构造菱形
为顶点构造菱形![]() .
.
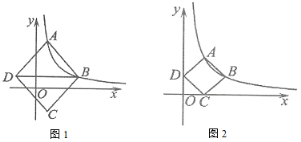
(1)如图1,点![]() ,
,![]() 横坐标分别为1,4,对角线
横坐标分别为1,4,对角线![]() 轴,菱形
轴,菱形![]() 面积为
面积为![]() .求
.求![]() 的值.
的值.
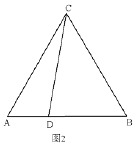
(2)如图2,当点![]() ,
,![]() 运动至某一时刻,点
运动至某一时刻,点![]() ,点
,点![]() 恰好落在
恰好落在![]() 轴和
轴和![]() 轴正半轴上,此时
轴正半轴上,此时![]() .求点
.求点![]() ,
,![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)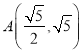 ,
,
【解析】
(1) 由菱形的性质可得BD=2BE=6, AC⊥DB,由菱形的面积公式可求AC=![]() ,设点B (4,a),则点A (1,
,设点B (4,a),则点A (1, ![]() +a),代入解析式可求a的值,即可求k的值;
+a),代入解析式可求a的值,即可求k的值;
(2)过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,设点A (m, ![]() ),由全等三角形的性质可得AE=DO=CF=m, DE=OC=BF=
),由全等三角形的性质可得AE=DO=CF=m, DE=OC=BF=![]() -m,可求点B坐标,代入解析式可求解.
-m,可求点B坐标,代入解析式可求解.
(1)如图,连结![]() 交
交![]() 于点
于点![]() .
.
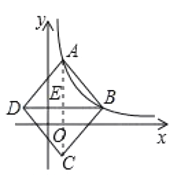
∵![]() ,
,![]() 的横坐标分别为1,4,
的横坐标分别为1,4,![]() 轴.
轴.
∴![]()
∵菱形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]()
∴![]() ,AC⊥DB
,AC⊥DB
∵![]()
∴![]()
∴AE=CE=![]()
设![]() ,
,![]()
∵点![]() ,
,![]() 都在反比例函数
都在反比例函数![]() 上
上
∴![]() 解得
解得![]() .
.
∴![]() .
.
(2)如图,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴.
轴.
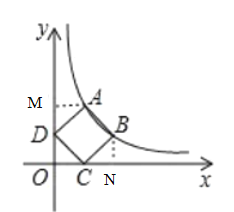
由(1)可知点![]() ,
,![]() 在反比例函数
在反比例函数![]() 上,设
上,设![]()
∵菱形![]() 中,
中,![]()
∴四边形![]() 是正方形
是正方形
∴![]() ,
,![]()
∴∠ADM+∠MAD=90°,∠MDA+∠CDO=90°,∠DCO+∠CDO=90°,∠BCN+∠DCO=90°,
∴∠MAD=∠CDO=∠BCN,且∠AMD=∠DOC=∠CNB90°,AD=CD=BC,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() .
.
由此可知点![]() 的坐标为
的坐标为![]() ,
,
将点![]() 代入
代入![]() 得
得![]()
![]() 或
或![]() (舍去)
(舍去)
∴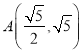 ,
,


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】初三第一轮复习重在查漏补缺,课后很重要的一项任务是“纠错”.在深大附中九年级随机抽取部分学生进行调查,对平时的错题:![]() 表示“每一道错题都解决了”,
表示“每一道错题都解决了”,![]() 表示“大部分错题解决了”,
表示“大部分错题解决了”,![]() 表示“只有一部分错题解决了”,
表示“只有一部分错题解决了”,![]() 表示“从不解决错题”.对抽取的学生问卷统计后如图:
表示“从不解决错题”.对抽取的学生问卷统计后如图:
(1)抽查的学生有______人;扇形统计图中,![]() 占比_______;
占比_______;![]() 占比_______.
占比_______.
(2)补全条形统计图;
(3)全年级有480人,估计对错题“全解决”和“大部分解决”共有多少学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 如图所示,它与二次函数y=ax2-2ax+c的图像交于A、B两点(其中点A在点B的左侧),与这个二次函数图像的对称轴交于点C.
如图所示,它与二次函数y=ax2-2ax+c的图像交于A、B两点(其中点A在点B的左侧),与这个二次函数图像的对称轴交于点C.
(1)求点C的坐标;
(2)设二次函数图像的顶点为D.若AD的垂直平分线经过点C,且![]() .求此二次函数的关系式.
.求此二次函数的关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉锁与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为![]() 轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (m,n 为常数).
(m,n 为常数).
(1)若抛物线的的对称轴为直线 x=1,且经过点(0,-1),求 m,n 的值;
(2)若抛物线上始终存在不重合的两点关于原点对称,求 n 的取值范围;
(3)在(1)的条件下,存在正实数 a,b( a<b),当 a≤x≤b 时,恰好有![]() ,请直接写出 a,b 的值.
,请直接写出 a,b 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽量减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件,
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2)当每件衬衫降价多少元时,商场每天获利最大,每天获利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
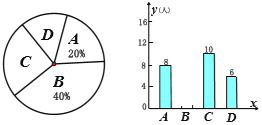
【题目】如图,在平面直角坐标系中,函数y=![]() (x>0)的图象经过菱形OACD的顶点D和边AC上的一点E,且CE=2AE,菱形的边长为8,则k的值为_____.
(x>0)的图象经过菱形OACD的顶点D和边AC上的一点E,且CE=2AE,菱形的边长为8,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数![]() (a,b为常数,且
(a,b为常数,且![]() )与反比例函数
)与反比例函数![]() (m为常数,且
(m为常数,且![]() )的图象交于点A(﹣2,1)、B(1,n).
)的图象交于点A(﹣2,1)、B(1,n).

(1)求反比例函数和一次函数的解析式;
(2)连结OA、OB,求△AOB的面积;
(3)直接写出当![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
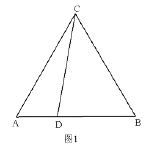
【题目】已知![]() 为等边三角形,点
为等边三角形,点![]() 是线段
是线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合).将线段
重合).将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连结
,连结![]() ,
,![]() .
.
(1)依题意补全图1并判断![]() 与
与![]() 的数量关系.
的数量关系.
(2)过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,用等式表示线段
,用等式表示线段![]() ,
,![]() 与
与![]() 之间的数量关系并证明.
之间的数量关系并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com