
| 5 |
| 3 |
| 4 |

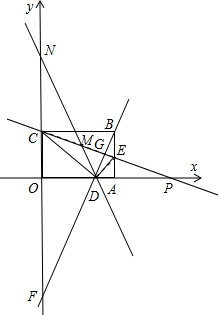 ∴△OCD∽△ADE.
∴△OCD∽△ADE.| AE |
| AD |
| 3 |
| 4 |
| OC |
| AD |
| CD |
| DE |
| 8t |
| 4t |
| CD |
| 5t |
| 5 |
|
|
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
| ||
| 2 |
 说明理由.
说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| x(页) | 100 | 200 | 400 | 1000 | … |
| y(元) | 40 | 80 | 160 | 400 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 轴正半轴于点Q(如图).
轴正半轴于点Q(如图).| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 承担的总费用如表②所示.
承担的总费用如表②所示.| 年住院费 | 承担办法 |
| 不超过5000元的部分 | 个人承担c%,其余由村集体承担 |
| 超过5000元但不超过20000元的部分 | 个人承担d%,其余由村集体承担 |
| 超过2000元的部分 | 全部由村集体承担 |
| 村民 | 门诊费(元) | 住院费(元) | 年个人承担总费用(元) |
| 甲 | 20 | 0 | 60 |
| 乙 | 160 | 0 | 60 |
| 丙 | 260 | 0 | 80 |
| 丁 | 70 | 800 | 380 |
| 戊 | 280 | 6000 | 2300 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 走的路程y(千米)随时间x(分钟)变化的函数图象.
走的路程y(千米)随时间x(分钟)变化的函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com