
【题目】已知:在平面直角坐标系xOy中,二次函数![]()
![]() 的图像与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.
的图像与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.
(1)求这个二次函数的解析式;
(2)点D的坐标为![]() ,点P在二次函数的图像上,∠ADP为锐角,且
,点P在二次函数的图像上,∠ADP为锐角,且![]() ,请直接写出点P的横坐标;
,请直接写出点P的横坐标;
(3)点E在x轴的正半轴上,![]() ,点O与点
,点O与点![]() 关于EC所在直线对称,过点O作
关于EC所在直线对称,过点O作![]() 的垂线,垂足为点N,ON与EC交于点M.若
的垂线,垂足为点N,ON与EC交于点M.若![]() ,求点E的坐标.
,求点E的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)点E的坐标为
;(3)点E的坐标为![]()
【解析】
(1)根据对称轴坐标公式可求二次函数图象的对称轴,当![]() 时,
时,![]() ,可求点C的坐标为
,可求点C的坐标为![]() ,根据三角形面积公式可求
,根据三角形面积公式可求![]() ,进一步得到A点和B点的坐标分别为
,进一步得到A点和B点的坐标分别为![]() ,
,![]()
![]() ,再用待定系数法即可求二次函数的解析式;
,再用待定系数法即可求二次函数的解析式;
(2)作![]() 轴于点F.分两种情况:(ⅰ)当点P在直线AD的下方时;(ⅱ)当点P在直线AD的上方时,延长
轴于点F.分两种情况:(ⅰ)当点P在直线AD的下方时;(ⅱ)当点P在直线AD的上方时,延长![]() 至点G使得
至点G使得![]() ,连接DG,作
,连接DG,作![]() 轴于点H,两种情况讨论可求点
轴于点H,两种情况讨论可求点![]() 的坐标;
的坐标;
(3)连接![]() ,交CE于T.连接
,交CE于T.连接![]() ,根据三角函数的整数可得
,根据三角函数的整数可得![]() ,同理
,同理![]() ,得到
,得到![]() ,从而得到点E的坐标.
,从而得到点E的坐标.
(1)当x = 0时,![]() ,∴
,∴ ![]() ,
,
∵ ![]() ,∴ AB = 6,
,∴ AB = 6,
又∵ 二次函数图像的对称轴是直线![]() ,
,
∴ ![]() ,
,![]() ,
,
∴ ![]() ,解得
,解得![]() ,
,
∴ 二次函数的解析式为![]() ,
,
(2)如图,作![]() 轴于点F.分两种情况:
轴于点F.分两种情况:
(ⅰ)当点P在直线AD的下方时,如图所示,
由(1)得点![]() ,点
,点![]() ,
,
∴DF=1,AF=2,
在Rt△ADF中,,![]() ,得
,得![]() .
.
延长DF与抛物线交于点![]() ,则
,则![]() 点即为所求.
点即为所求.
将x=-2代入抛物线解析式,得y=-4,
∴点![]() 的坐标为
的坐标为![]() .
.
(ⅱ)当点P在直线AD的上方时,延长![]() 至点G使得
至点G使得![]() ,连接DG,作
,连接DG,作![]() 轴于点H,如图所示,在
轴于点H,如图所示,在![]() 与
与![]() 中,
中,
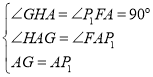
∴![]() ≌
≌![]() (AAS).
(AAS).
![]() ,
,![]()
又![]() ,
,![]()
∴点G的坐标是![]()
在![]() 中,
中, ![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
设DG与抛物线的交点为![]() ,则
,则![]() 点为所求.
点为所求.
作![]() 于点K,作
于点K,作![]() 交DK于点S.
交DK于点S.
设![]() 点的坐标为
点的坐标为![]() ,
,
则![]() ,
,
![]() .
.
由![]() ,
,![]() ,
,![]() ,得
,得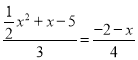 .
.
整理,得![]()
解得![]() .
.
![]() 点在第二象限,横坐标为负,
点在第二象限,横坐标为负,
![]() 点的横坐标为
点的横坐标为![]()
综上,P点的横坐标为![]() 或
或![]() .
.
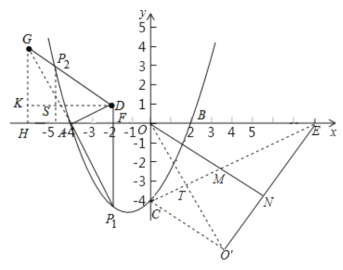
(3)如图,联结![]() ,交EC于点T,联结
,交EC于点T,联结![]() .
.
∵ 点O与点![]() 关于EC所在直线对称,
关于EC所在直线对称,
∴ ![]() ⊥EC,
⊥EC,![]() ,
,![]() .
.
∴ ![]() ⊥
⊥![]()
又∵ ON⊥![]() ,∴
,∴ ![]() ∥ON.
∥ON.
∴ ![]() .
.
∴ OC = OM
∴ CT = MT
在Rt△ETO中,∠ETO = 90°,![]() .
.
在Rt△COE中,∠COE = 90°,![]() .
.
∴ ![]()
∴ ![]()
同理可得![]()
∴ ![]()
∵ ![]() ,∴ OE = 8
,∴ OE = 8
∵ 点E在x轴的正半轴上
∴ 点E的坐标为![]() .
.


科目:初中数学 来源: 题型:
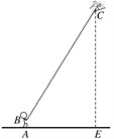
【题目】小明在海湾森林公园放风筝.如图所示,小明在A处,风筝飞到C处,此时线长BC为40米,若小明双手牵住绳子的底端B距离地面1.5米,从B处测得C处的仰角为60°,求此时风筝离地面的高度CE.(计算结果精确到0.1米,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
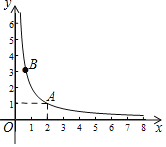
【题目】如图,在平面直角坐标系![]() 中的第一象限内,反比例函数图象过点
中的第一象限内,反比例函数图象过点![]() 和另一动点
和另一动点![]() .
.
(1)求此函数表达式;
(2)如果![]() ,写出
,写出![]() 的取值范围;
的取值范围;
(3)直线![]() 与坐标轴交于点
与坐标轴交于点![]() ,如果
,如果![]() ,直接写出点
,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在“五一”促销活动中规定,顾客每消费100元就能获得一次中奖机会.为了活跃气氛.设计了两个抽奖方案:
方案一:转动转盘![]() 一次,转出红色可领取一份奖品;
一次,转出红色可领取一份奖品;
方案二:转动转盘![]() 两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
两次,两次都转出红色可领取一份奖品.(两个转盘都被平均分成3份)
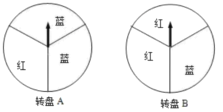
(1)若转动一次![]() 转盘,求领取一份奖品的概率;
转盘,求领取一份奖品的概率;
(2)如果你获得一次抽奖机会,你会选择哪个方案?请采用列表法或树状图说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上, 顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为__ _.

查看答案和解析>>
科目:初中数学 来源: 题型:
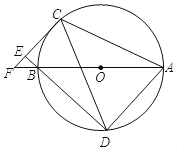
【题目】如图,AB为⊙O的直径,C、D为⊙O上异于A、B的两点,连接CD,过点C作CE⊥DB,交CD的延长线于点E,垂足为点E,直径AB与CE的延长线相交于点F.
(1)连接AC,AD,求证:∠DAC+∠ACF=180°;
(2)若∠ABD=2∠BDC,
①求证:CF是⊙O的切线;
②当BD=6,tanF=![]() 时,求CF的长.
时,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了求1+2+22+23+…+22016+22017的值,
可令S=1+2+22+23+…+22016+22017,
则2S=2+22+23+24+…+22017+22018,
因此2S﹣S=22018﹣1,
所以1+22+23+…+22017=22018﹣1.
请你仿照以上方法计算1+5+52+53+…+52017的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,直线
,直线![]() 与y轴交于点A,与双曲线
与y轴交于点A,与双曲线![]() 交于点
交于点![]() .
.
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若![]() 的面积为6,求直线CD的表达式.
的面积为6,求直线CD的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
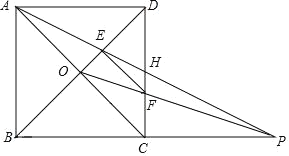
【题目】如图,正方形ABCD的边长为1.对角线AC、BD相交于点O,P是BC延长线上的一点,AP交BD于点E,交CD于点H,OP交CD于点F,且EF与AC平行.
(1)求证:EF⊥BD.
(2)求证:四边形ACPD为平行四边形.
(3)求OF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com