
【题目】在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() )的图象G与直线
)的图象G与直线![]() 交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
(1)求![]() 的值;
的值;
(2)横、纵坐标都是整数的点叫做整点.记图象![]() 与直线l围成的区域(不含边界)为W.
与直线l围成的区域(不含边界)为W.
①当n=5时,求![]() 的值,并写出区域W内的整点个数;
的值,并写出区域W内的整点个数;
②若区域W内恰有5个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)m=4;(2)①区域![]() 内有2个整点;②
内有2个整点;②![]()
【解析】
(1)把点A的坐标代入反比例函数解析式求解即可;
(2)①先求出当n=5时![]() 的值,然后结合函数图象解答即可;
的值,然后结合函数图象解答即可;
②如图2,分别求出当n=6、n=7时k的值,再结合函数图象求出区域![]() 内的整点个数,进而可判断当n≥8时区域
内的整点个数,进而可判断当n≥8时区域![]() 内的整点个数,从而可得结果.
内的整点个数,从而可得结果.
解:(1)∵点A(4,1)在函数![]() (
(![]() )的图象G上,
)的图象G上,
∴ m= 4;
(2)①当n=5时,直线![]() 经过点B(1,5),
经过点B(1,5),
∴ ![]() ,解得
,解得![]() .
.
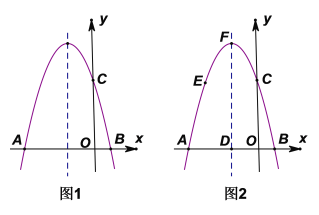
此时区域![]() 内有2个整点(2,3)、(3,2),如图1;
内有2个整点(2,3)、(3,2),如图1;

②如图2,∵直线![]() 过定点A(4,1),n为整数,
过定点A(4,1),n为整数,
∴当n=6时,直线![]() 经过点B(1,6),解得
经过点B(1,6),解得![]() ,此时区域
,此时区域![]() 内有4个整点;
内有4个整点;
当n=7时,直线![]() 经过点B(1,7),解得
经过点B(1,7),解得![]() ,区域
,区域![]() 内有5个整点;
内有5个整点;
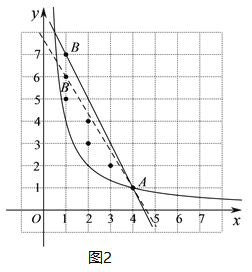
∴ ![]() 的取值范围是
的取值范围是![]() .
.


科目:初中数学 来源: 题型:
【题目】正方形![]() 的边长为4,点
的边长为4,点![]() 在对角线
在对角线![]() 上(可与点
上(可与点![]() 重合),
重合),![]() ,点
,点![]() 在正方形的边上.下面四个结论中,
在正方形的边上.下面四个结论中,
①存在无数个四边形![]() 是平行四边形;
是平行四边形;
②存在无数个四边形![]() 是菱形;
是菱形;
③存在无数个四边形![]() 是矩形;
是矩形;
④至少存在一个四边形![]() 是正方形.
是正方形.
所有正确结论的序号是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
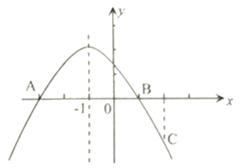
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() 点
点![]() ,点
,点![]() 点
点![]() 是抛物线上任意一点,有下列结论:①
是抛物线上任意一点,有下列结论:①![]() ; ②一元二次方程
; ②一元二次方程![]() 的两个根为
的两个根为![]() 和
和![]() ;③若
;③若![]() ,则
,则![]() ;④对于任意实数
;④对于任意实数![]()
![]() 总成立.其中正确结论的个数为 ( )
总成立.其中正确结论的个数为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校按照开展“阳光体育运动”的要求,决定主要开设![]() :乒乓球、
:乒乓球、![]() :篮球、
:篮球、![]() :跑步
:跑步![]() :跳绳这四种运动项目.为了了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题:
:跳绳这四种运动项目.为了了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图和扇形统计图.请你结合图中的信息解答下列问题:
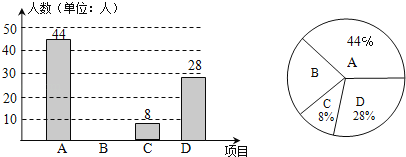
(1)样本中喜欢![]() 项目的人数百分比是多少?其所在扇形统计图中的圆心角的度数是多少?
项目的人数百分比是多少?其所在扇形统计图中的圆心角的度数是多少?
(2)把条形统计图补充完整;
(3)已知该校有1000人,请根据样本估计全校喜欢乒乓球的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“在已知三角形的一边上取一点,使得这点到这个三角形的另外两边的距离相等”的尺规作图过程:
已知:△ABC.
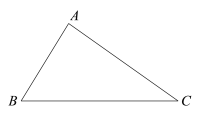
求作:点D,使得点D在BC边上,且到AB,AC边的距离相等.
作法:如图,
作∠BAC的平分线,交BC于点D.则点D即为所求.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形 (保留作图痕迹);
(2)完成下面的证明.
证明:作DE⊥AB于点E,作DF⊥AC于点F,
∵AD平分∠BAC,
∴ = ( ) (填推理的依据) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师将自己2019年10月至2020年5月的通话时长(单位:分钟)的有关数据整理如下:
①2019年10月至2020年3月通话时长统计表
时间 | 10月 | 11月 | 12月 | 1月 | 2月 | 3月 |
时长(单位:分钟) | 520 | 530 | 550 | 610 | 650 | 660 |
②2020年4月与2020年5月,这两个月通话时长的总和为1100分钟根据以上信息,推断张老师这八个月的通话时长的中位数可能的最大值为( )
A.550B.580C.610D.630
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() )的图象G与直线
)的图象G与直线![]() 交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
(1)求![]() 的值;
的值;
(2)横、纵坐标都是整数的点叫做整点.记图象![]() 与直线l围成的区域(不含边界)为W.
与直线l围成的区域(不含边界)为W.
①当n=5时,求![]() 的值,并写出区域W内的整点个数;
的值,并写出区域W内的整点个数;
②若区域W内恰有5个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]()
![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() 、
、![]() 两点间的距离为
两点间的距离为![]() ,抛物线的对称轴为
,抛物线的对称轴为![]() .
.
(1)求抛物线的解析式;
(2)如图1,对称轴上是否存在点![]() ,使
,使![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)如图2,抛物线的顶点为![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]() ,点
,点![]() 为抛物线上一点,点
为抛物线上一点,点![]() 不与点
不与点![]() 重合. 当
重合. 当![]() 时,过点
时,过点![]() 分别作
分别作![]() 轴的垂线和平行线,与
轴的垂线和平行线,与![]() 轴交于点
轴交于点![]() 、与对称轴交于点
、与对称轴交于点![]() ,得到矩形
,得到矩形![]() ,求矩形
,求矩形![]() 周长的最大值;
周长的最大值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com