阅读：
如图，已知在△ABC和△A′B′C′中，AB=A′B′，∠A=∠A′，AC=A′C′．那么△ABC≌△A′B′C′．
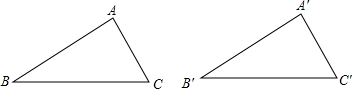
说明过程如下：
把△ABC放到△A′B′C′上，使∠A的顶点与∠A′的顶点重合；由于∠A=∠A′，因此可以使射线AB、AC分别落在射线A′B′、A′C′上．因为AB=A′B′，AC=A′C′，所以点B、C分别与点B′、C′重合，这样△ABC和△A′B′C′重合，即△ABC≌△A′B′C′．
于是，得全等三角形判定方法1：在两个三角形中，如果有两条边及它们的夹角对应相等，那么这两个三角形全等（简记为S．A．S）．
请完成下面问题的填空：
如图，已知在△ABC和△A′B′C′中，∠A=∠A′，AB=A′B′∠B=∠B′．
那么△ABC≌△A′B′C′．
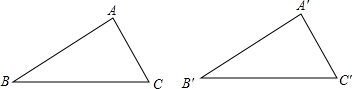
说明过程如下：
把△ABC放到△A′B′C′上，因为AB=A′B′，可以使
AB
AB
与
A′B′
A′B′
重合，并使点C与C′在AB（A′B′）的同一侧，这时点A与点A′重合，点
C
C
与点
C′
C′
重合．由于∠A=∠A′，因此射线
AC
AC
与射线
A′C′
A′C′
叠合；由于
∠B=∠B′，因此射线
BC
BC
与射线
B′C′
B′C′
叠合．于是点C（射线AC与BC的交点）与点C（射线A′C′与B′C′的交点）重合．这样
△ABC
△ABC
与
△A′B′C′
△A′B′C′
重合，即△ABC≌△A′B′C′．
于是，得全等三角形判定方法2：在两个三角形中，
如果两角和它们的夹边对应相等，那么这两个三角形全等（简记为ASA）
如果两角和它们的夹边对应相等，那么这两个三角形全等（简记为ASA）
．
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
