
【题目】《朗读者》自播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,沭阳县某中学开展“朗读”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示。
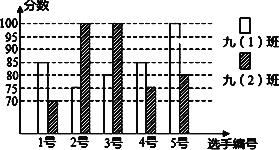
⑴根据图示填写表格;
平均数 | 中位数 | 众数 | |
九⑴班 | 85 | 85 | |
九⑵班 | 80 |
⑵如果规定成绩较稳定的班级胜出,你认为哪个班级能胜出?说明理由。
【答案】(1)85;85;100;(2)九(1)班的成绩更稳定,能胜出.
【解析】
(1)由条形图得出两班的成绩,根据中位数、平均数及众数分别求解可得;
(2)分别计算两班成绩的方差,由方差小的成绩稳定解答.
(1)九(1)班5位同学的成绩为:75、80、85、85、100,
∴其中位数为85分;
九(2)班5位同学的成绩为:70、100、100、75、80,
∴九(2)班的平均数为![]() =85(分),其众数为100分,
=85(分),其众数为100分,
补全表格如下:
平均数 | 中位数 | 众数 | |
九(1)班 | 85 | 85 | 85 |
九(2)班 | 85 | 80 | 100 |
(2)九(1)班的成绩更稳定,能胜出.
∵S九(1)2=![]() ×[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70(分2),
×[(75-85)2+(80-85)2+(85-85)2+(85-85)2+(100-85)2]=70(分2),
S九(2)2=![]() ×[(70-85)2+(100-85)2+(100-85)2+(75-85)2+(80-85)2]=160(分2),
×[(70-85)2+(100-85)2+(100-85)2+(75-85)2+(80-85)2]=160(分2),
∴S九(1)2<S九(2)2,
∴九(1)班的成绩更稳定,能胜出.


科目:初中数学 来源: 题型:
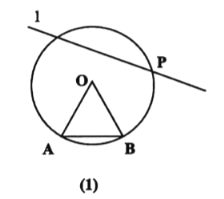
【题目】(一)如图(1),已知圆![]() ,点
,点![]() 、
、![]() 在圆上,且
在圆上,且![]() 为等边三角形,点
为等边三角形,点![]() 为直线
为直线![]() 与圆
与圆![]() 的一个交点.连接
的一个交点.连接![]() ,
,![]() ,证明:
,证明:![]()
(方法迁移)
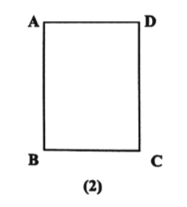
(二)如图(2),用直尺和圆规在矩形![]() 内作出所有的点
内作出所有的点![]() ,使得
,使得![]() (不写作法,保留作图痕迹).
(不写作法,保留作图痕迹).
(深入探究)
(三)已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 边上的点,若满足
边上的点,若满足![]() 的点P恰有两个,求
的点P恰有两个,求![]() 的取值范围.
的取值范围.
(四)已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 为矩形
为矩形![]() 内一点,且
内一点,且![]() ,若点
,若点![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 到点
到点![]() ,求
,求![]() 的最小值,并求此时
的最小值,并求此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为C与x轴交于A、B两点(点A在点B左侧),点C、B关于过点A的直线l:y=kx+![]() 对称.
对称.
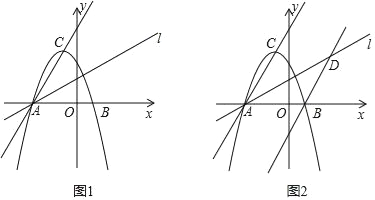
(1)求A、B两点坐标及直线l的解析式;
(2)求二次函数解析式;
(3)如图2,过点B作直线BD∥AC交直线l于D点,M、N分别为直线AC和直线l上的两个动点,连接CN,MM、MD,求CN+NM+MD的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示△ABC中,∠C=90°,∠A,∠B的平分线交于D点,DE⊥BC于点E,DF⊥AC于点F.
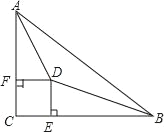
(1)求证:四边形CEDF为正方形;
(2)若AC=6,BC=8,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=60°,∠ABC=45°,AB=![]() ,D是线段BC上的一个动点,以AD为直径画圆O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为( )
,D是线段BC上的一个动点,以AD为直径画圆O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为( )
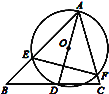
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() .
.
(1)若点![]() 也在该抛物线上,请用含
也在该抛物线上,请用含![]() 的关系式表示
的关系式表示![]() ;
;
(2)若该抛物线上任意不同两点![]() 、
、![]() 都满足:当
都满足:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;若以原点
;若以原点![]() 为圆心,
为圆心,![]() 为半径的圆与抛物线的另两个交点为
为半径的圆与抛物线的另两个交点为![]() 、
、![]() (点
(点![]() 在点
在点![]() 左侧),且
左侧),且![]() 有一个内角为
有一个内角为![]() ,求抛物线的解析式;
,求抛物线的解析式;
(3)在(2)的条件下,若点![]() 与点
与点![]() 关于点
关于点![]() 对称,且
对称,且![]() 、
、![]() 、
、![]() 三点共线,求证:
三点共线,求证:![]() 平分
平分![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCO是平行四边形,OA=1,AB=3,点C在x轴的负半轴上,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,点F恰好落在x轴的正半轴上,则D点的坐标为( )
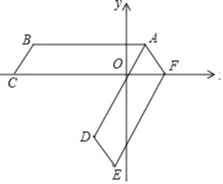
A.(1,![]() )B.(﹣1,﹣
)B.(﹣1,﹣![]() )C.(
)C.(![]() ,1)D.(﹣
,1)D.(﹣![]() ,﹣1)
,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
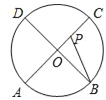
A. 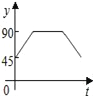 B.
B.  C.
C. 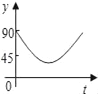 D.
D. 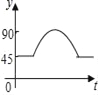
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com