
【题目】如图,在正方形![]() 中,点
中,点![]() 是
是![]() 上一动点(不写
上一动点(不写![]() 重合),对角线
重合),对角线![]() 相交于点
相交于点![]() ,过点
,过点![]() 分别作
分别作![]() 的垂线,分别交
的垂线,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,下列结论:①
,下列结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]()
![]()
![]() ;④当
;④当![]()
![]()
![]() 时,点
时,点![]() 是
是![]() 的中点,其中一定正确的结论有_______.(填上所有正确的序号)
的中点,其中一定正确的结论有_______.(填上所有正确的序号)
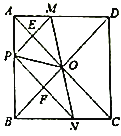
【答案】①②④
【解析】
①根据正方形的每一条对角线平分一组对角可得∠PAE=∠MAE=45°,然后利用“角边角”证明△APE和△AME全等;②根据全等三角形对应边相等可得PE=EM=![]() PM,同理,FP=FN=
PM,同理,FP=FN=![]() NP,证出四边形PEOF是矩形,得出PF=OE,证得△APE为等腰直角三角形,得出AE=PE,PE+PF=OA,即可得到PM+PN=AC;③判断出△POF不一定等腰直角三角形,△BNF是等腰直角三角形,从而确定出两三角形不一定相似;④证出△APM和△BPN以及△APE、△BPF都是等腰直角三角形,从而得出结论.
NP,证出四边形PEOF是矩形,得出PF=OE,证得△APE为等腰直角三角形,得出AE=PE,PE+PF=OA,即可得到PM+PN=AC;③判断出△POF不一定等腰直角三角形,△BNF是等腰直角三角形,从而确定出两三角形不一定相似;④证出△APM和△BPN以及△APE、△BPF都是等腰直角三角形,从而得出结论.
①∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°,
∵PM⊥AC,
∴∠AEP=∠AEM=90°,
在△APE和△AME中,
∵![]() ,
,
![]() ,
,
![]() ,
,
∴△APE≌△AME(ASA),
故①正确;
②∵△APE≌△AME,
∴PE=EM=![]() PM,
PM,
同理,FP=FN=![]() NP,
NP,
∵正方形ABCD中,AC⊥BD,
又∵PE⊥AC,PF⊥BD,
∴∠PEO=∠EOF=∠PFO=90°,且△APE中AE=PE
∴四边形PEOF是矩形.
∴PF=OE,
∵在△APE中,∠AEP=90°,∠PAE=45°,
∴△APE为等腰直角三角形,
∴AE=PE,
∴PE+PF=OA,
又∵PE=EM=![]() PM,FP=FN=
PM,FP=FN=![]() NP,OA=
NP,OA=![]() AC,
AC,
∴PM+PN=AC,
故②正确;
③∵△APE≌△AME,
∴AP=AM
△BNF是等腰直角三角形,而△POF不一定是,
∴△POF与△BNF不一定相似,
故④错误;
④∵△APE≌△AME,
∴AP=AM,
∴△AMP是等腰直角三角形,
同理,△BPN是等腰直角三角形,
当△PMN∽△AMP时,△PMN是等腰直角三角形.
∴PM=PN,
又∵△AMP和△BPN都是等腰直角三角形,
∴AP=BP,即P是AB的中点,
故④正确;
故答案为①②④.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线的顶点为![]() ,且经过点
,且经过点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点.
两点.
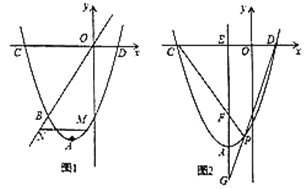
(1)求直线![]() 和抛物线的函数表达式;
和抛物线的函数表达式;
(2)如图,点![]() 是抛物线上的一个动点,且在直线
是抛物线上的一个动点,且在直线![]() 的下方,过点
的下方,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)如图,过点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,且
,且![]() 轴,点
轴,点![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一个动点,直线
之间的一个动点,直线![]() 、
、![]() 与
与![]() 分别交于
分别交于![]() 、
、![]() 两点.当点
两点.当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
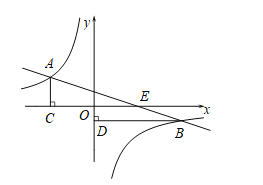
【题目】如图,点A(-3,2)和点B(m,n)在反比例函数y=![]() (k≠0)的图象上(其中m>0),AC⊥x轴,垂足为C,BD⊥y轴,垂足为D,直线AB与x轴相交于点E.
(k≠0)的图象上(其中m>0),AC⊥x轴,垂足为C,BD⊥y轴,垂足为D,直线AB与x轴相交于点E.
(1)写出反比例函数表达式;
(2)求tan∠ABD(用含m的代数式表示);
(3)若CE=6,直接写出B点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
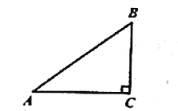
【题目】如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.

(1)求BD·cos∠HBD的值;
(2)若∠CBD=∠A,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6,AD=8,点E是边AD上一点,EM⊥BC交AB于点M,点N在射线MB上,且AE是AM和AN的比例中项.
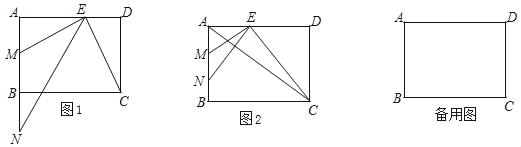
(1)如图1,求证:∠ANE=∠DCE;
(2)如图2,当点N在线段MB之间,联结AC,且AC与NE互相垂直,求MN的长;
(3)连接AC,如果△AEC与以点E、M、N为顶点所组成的三角形相似,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
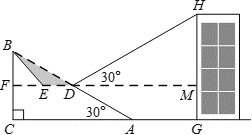
【题目】如图,已知斜坡![]() 长
长![]() 米,坡角(即
米,坡角(即![]() )为
)为![]() ,
,![]() ,现计划在斜坡中点
,现计划在斜坡中点![]() 处挖去部分坡体(用
处挖去部分坡体(用![]() 表示)修建一个平行于水平线
表示)修建一个平行于水平线![]() 的平台
的平台![]() 和一条新的斜坡
和一条新的斜坡![]() (结果精确到
(结果精确到![]() ,参考数据
,参考数据![]() ).
).
(1)若修建的斜坡![]() 的坡角(即
的坡角(即![]() )不大于
)不大于![]() ,则平台
,则平台![]() 的长最多为______米?(直接写出结果)
的长最多为______米?(直接写出结果)
(2)一座建筑物![]() 距离坡角
距离坡角![]() 点
点![]() 米远(即
米远(即![]() 米),小明在
米),小明在![]() 点测得建筑物顶部
点测得建筑物顶部![]() 的仰角(即
的仰角(即![]() )为
)为![]() ,点
,点![]() 在同一平面内,点
在同一平面内,点![]() 在同一条直线上,且
在同一条直线上,且![]() ,问建筑物
,问建筑物![]() 高为多少米?
高为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地在进入防汛期间,准备对4800米长的河堤进行加固,在加固工程中,该地驻军出色地完成了任务,它们在加固600米后,采用了新的加固模式,每天加固的长度是原来的2倍,结果只用9天就完成了加固任务.
(1)求该地驻军原来每天加固大坝的米数;
(2)由于汛情严重,该驻军部队又接到了加固一段长4200米大坝的任务,他们以上述新的加固模式进行了2天后,接到命令,必须在4天内完成剩余任务,求该驻军每天至少还要再多加固多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,先将
,先将![]() 绕着顶点
绕着顶点![]() 顺时针旋转
顺时针旋转![]() ,然后再将旋转后的三角形进行放大或缩小得到
,然后再将旋转后的三角形进行放大或缩小得到![]() (点
(点![]() 的对应点分别是点
的对应点分别是点![]() ),联结
),联结![]() ,如果
,如果![]() 和
和![]() 相似,那么
相似,那么![]() 的长是__________.
的长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蔬菜基地种植了娃娃菜和油菜两种蔬菜共![]() 亩,设种植娃娃菜
亩,设种植娃娃菜![]() 亩,总收益为
亩,总收益为![]() 万元,有关数据见下表:
万元,有关数据见下表:
成本(单位:万元/亩) | 销售额(单位:万元/亩) | |
娃娃菜 | 2.4 | 3 |
油菜 | 2 | 2.5 |
(1)求![]() 关于
关于![]() 的函数关系式(收益 = 销售额 – 成本);
的函数关系式(收益 = 销售额 – 成本);
(2)若计划投入的总成本不超过![]() 万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
(3)已知娃娃菜每亩地需要化肥![]() kg,油菜每亩地需要化肥
kg,油菜每亩地需要化肥![]() kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的
kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的![]() 倍,结果运送完全部化肥的次数比原计划少
倍,结果运送完全部化肥的次数比原计划少![]() 次,求基地原计划每次运送多少化肥.
次,求基地原计划每次运送多少化肥.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com