
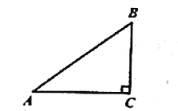
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,先将
,先将![]() 绕着顶点
绕着顶点![]() 顺时针旋转
顺时针旋转![]() ,然后再将旋转后的三角形进行放大或缩小得到
,然后再将旋转后的三角形进行放大或缩小得到![]() (点
(点![]() 的对应点分别是点
的对应点分别是点![]() ),联结
),联结![]() ,如果
,如果![]() 和
和![]() 相似,那么
相似,那么![]() 的长是__________.
的长是__________.
【答案】3![]() -5
-5
【解析】
由题意当点A′在线段BC上且AA′平分∠BAC时,△AA′B和△AA′B′相似,作A′H⊥AB于H.证明△AA′H≌△AA′C(AAS),推出A′C=A′H,AC=AH=2![]() ,设A′C=A′H=x,根据勾股定理构建方程即可解决问题.
,设A′C=A′H=x,根据勾股定理构建方程即可解决问题.
由题意当点A′在线段BC上且AA′平分∠BAC时,△AA′B和△AA′B′相似,作A′H⊥AB于H.

在Rt△ABC中,∵cosB=![]() =
=![]() ,AB=6,
,AB=6,
∴BC=4,AC=![]() =2
=2![]() ,
,
∵∠A′AH=∠A′AC,∠AHA′=∠ACA′=90°,AA′=AA′,
∴△AA′H≌△AA′C(AAS),
∴A′C=A′H,AC=AH=2![]() ,
,
设A′C=A′H=x,
在Rt△A′BH中,(4-x)2=x2+(6-2![]() )2,
)2,
∴x=3![]() -5,
-5,
∴A′C=3![]() -5,
-5,
故答案为:3![]() -5.
-5.


科目:初中数学 来源: 题型:
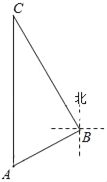
【题目】我国北斗导航装备的不断更新,极大方便人们的出行.光明中学组织学生利用导航到“金牛山”进行研学活动,到达A地时,发现C地恰好在A地正北方向,且距离A地11.46千米.导航显示路线应沿北偏东60°方同走到B地,再沿北偏西37°方向走一段距离才能到达C地,求B,C两地的距离(精确到1千米).
(参考数据sin53°≈0.80,cos53°≈0.60,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
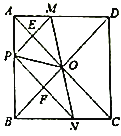
【题目】如图,在正方形![]() 中,点
中,点![]() 是
是![]() 上一动点(不写
上一动点(不写![]() 重合),对角线
重合),对角线![]() 相交于点
相交于点![]() ,过点
,过点![]() 分别作
分别作![]() 的垂线,分别交
的垂线,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,下列结论:①
,下列结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]()
![]()
![]() ;④当
;④当![]()
![]()
![]() 时,点
时,点![]() 是
是![]() 的中点,其中一定正确的结论有_______.(填上所有正确的序号)
的中点,其中一定正确的结论有_______.(填上所有正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )
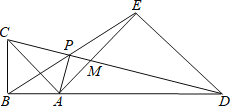
A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
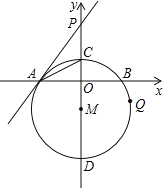
【题目】如图,在直角坐标系中,⊙M的圆心M在y轴上,⊙M与x轴交于点A、B,与y轴交于点C、D,过点A作⊙M的切线AP交y轴于点P,若点C的坐标为(0,2),点A的坐标为(-4,0),
(1)求证:∠PAC=∠CAO;
(2)求直线PA的解析式;
(3)若点Q为⊙M上任意一点,连接OQ、PQ,问![]() 的比值是否发生变化?若不变求出此值;若变化,说明变化规律.
的比值是否发生变化?若不变求出此值;若变化,说明变化规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
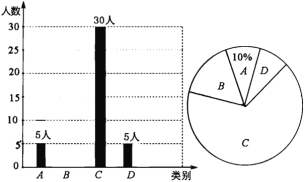
【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是_____________人,扇形统计图中C部分所对应的扇形圆心角的度数为_______.
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有__________人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为_____m2.

查看答案和解析>>
科目:初中数学 来源: 题型:
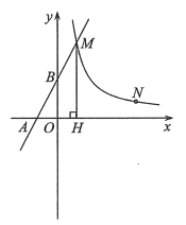
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与反比例函数
两点,与反比例函数![]() 的图像交于点
的图像交于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,且
,且![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图象上.
的图象上.
(1)求![]() 的值;
的值;
(2)在![]() 轴的正半轴上存在一点
轴的正半轴上存在一点![]() ,使得
,使得![]() 的值最小,求点
的值最小,求点![]() 的坐标;
的坐标;
(3)点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,把
,把![]() 向右平移
向右平移![]() 个单位到
个单位到![]() 的位置,当
的位置,当![]() 取得最小值时,请你在横线上直接写出
取得最小值时,请你在横线上直接写出![]() 的值,
的值,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
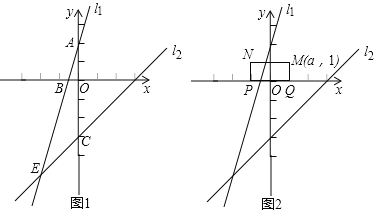
【题目】如图1,在直角坐标系中,一次函数的图象![]() 与
与![]() 轴交于点
轴交于点![]() ,与一次函数
,与一次函数![]() 的图象
的图象![]() 交于点
交于点![]() .
.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与y轴交于点
与y轴交于点![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)如图2,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() ,矩形
,矩形![]() 的边
的边![]() 在
在![]() 轴上平移,若矩形
轴上平移,若矩形![]() 与直线
与直线![]() 或
或![]() 有交点,直接写出
有交点,直接写出![]() 的取值范围,
的取值范围,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com