解:(1)当x=0时,y=6,
∴点C的坐标为C(0,6),
在Rt△AOC中,tan∠ACO=

,OC=6,
∴OA=1,
∴A(-1,0);
(2)∵OB=

OC,
∴OB=3,
∴B(3,0),
由题意,得
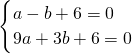
,
解得
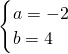
,
∴y=-2x
2+4x+6=-2(x-1)
2+8,
∴D(1,8),
设直线CD的解析式为y=kx+b,
则
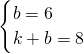
,
解得
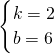
,
∴直线CD的解析式为y=2x+6,
∴点E的坐标为E(-3,0);
(3)假设存在以点A、C、F、E为顶点的平行四边形,
当AE为平行四边形的边时,F
1(2,6),F
2(-2,6),
当AE为平行四边形的对角线时,F
3(-4,-6),
经验证,只有点(2,6)在抛物线y=-2x
2+4x+6上,
∴F(2,6);
(4)如图,作NQ∥y轴交AM于点Q,
设N(m,-2m
2+4m+6),
当x=2时,y=6,
∴M(2,6),
设直线AM的解析式为y=kx+b,
则
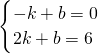
,
解得

,
∴直线AM的解析式为y=2x+2,
∴Q(m,2m+2),
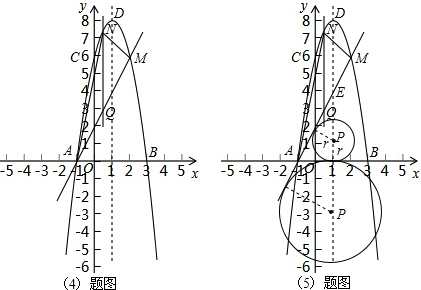
∴NQ=-2m
2+4m+6-(2m+2)=-2m
2+2m+4,
∵S
△ABM=

×4×6=12,
∴S=S
△ABM+S
△AMN=12+S
△ANQ+S
△MNQ,
=12+

×3×(-2m
2+2m+4),
=-3m
2+3m+18,
=-3(m-

)
2+
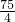
,
∴当m=

时,S的最大值为
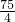
,
当m=

时,y=-2x
2+4x+6=-2×

+4×

+6=

,
∴N(

,

);
(5)设直线AM与对称轴相交于点E,
则y=2×1+2=4,
∴点E的坐标是(1,4),
∴AE=

=2

,
设圆的半径为r,
①圆心在x轴上方时,

=
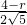
,
解得r=

-1,
∴点P的坐标为(1,

-1),
②圆心在x轴的下方时,

=
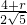
,
解得r=

+1,
∴点P的坐标为(1,-

-1),
综上所述,点P的坐标为(1,

-1)或(1,-

-1).
分析:(1)先令x=0求出点C的坐标,再利用三角函数值求出求出OA的值,从而得到点A的坐标;
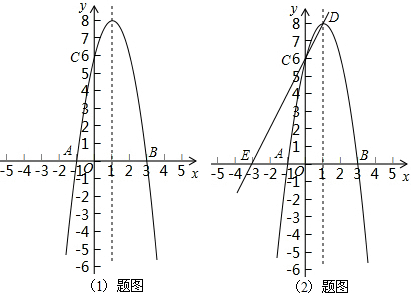
(2)求出OB的长度,得到点B的坐标,然后利用待定系数法求出抛物线的解析式,再求出顶点坐标D,再用待定系数法求出直线CD的解析式,就可以求出直线CD与x轴的交点E的坐标;
(3)根据AE是以点A、C、F、E为顶点的平行四边形的边或对角线可以求出对应F的坐标有3个,将三个坐标代入抛物线的解析式检验就可以确定在抛物线上的点F;
(4)过点N作NQ∥x轴交AM于点Q,根据抛物线的解析式设出点M的坐标,并求出点N的坐标,然后求出直线AM的解析式,再根据解析式以及点N的坐标设出点Q的坐标,然后表示出ABMN的面积S,再根据二次函数的最值问题进行解答即可;
(5)先求出直线AM与抛物线对称轴的交点E的坐标,利用勾股定理求出AE的长度,然后分①圆心在x轴上方②圆心在x轴的下方两种情况,根据相似三角形对应边成比例求出圆的半径r,写出点P的坐标即可.
点评:本题着重考查了待定系数法求二次函数解析式、二次函数的最值问题,平行四边形的判定和性质等知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.

 OC,tan∠ACO=
OC,tan∠ACO= ,顶点为D.
,顶点为D.
 ,OC=6,
,OC=6, OC,
OC,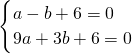 ,
,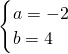 ,
, ∴D(1,8),
∴D(1,8),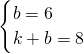 ,
,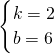 ,
,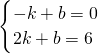 ,
, ,
,
 ×4×6=12,
×4×6=12, ×3×(-2m2+2m+4),
×3×(-2m2+2m+4), )2+
)2+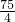 ,
, 时,S的最大值为
时,S的最大值为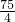 ,
, 时,y=-2x2+4x+6=-2×
时,y=-2x2+4x+6=-2× +4×
+4× +6=
+6= ,
, ,
, );
); =2
=2 ,
, =
=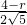 ,
, -1,
-1, -1),
-1), =
=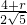 ,
, +1,
+1, -1),
-1), -1)或(1,-
-1)或(1,- -1).
-1).

 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=