
【题目】已知一个一次函数的图象与一个反比例函数的图象交于点![]() .
.
![]() 分别求出这两个函数的表达式;
分别求出这两个函数的表达式;
![]() 在同一个平面直角坐标系中画出这两个函数的图象,根据图象回答:当
在同一个平面直角坐标系中画出这两个函数的图象,根据图象回答:当![]() 取何值时,一次函数的值大于反比例函数的值?
取何值时,一次函数的值大于反比例函数的值?
![]() 求平面直角坐标中原点
求平面直角坐标中原点![]() 与
与![]() 点构成的三角形的面积.
点构成的三角形的面积.
【答案】(1)![]() ,
,![]() ;(2)图见详解,
;(2)图见详解,![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)设反比例的函数解析式为![]() ,一次函数的解析式为
,一次函数的解析式为![]() ,将点P代入
,将点P代入![]() 可得k值,将点Q代入可得m值,将点P、Q代入
可得k值,将点Q代入可得m值,将点P、Q代入![]() 求解即可;
求解即可;
(2)描点、连线即可画出函数的图象,当一次函数的图象在反比例函数图象的上方时,一次函数的值大于反比例函数的值,由此可确定x的取值;
(3)连接PO,QO,设直线与y轴交于点M,由![]() 求解.
求解.
解:(1)设反比例的函数解析式为![]() ,一次函数的解析式为
,一次函数的解析式为![]() ,
,
将点![]() 代入
代入![]() 得
得![]() ,解得
,解得![]() ,
,
![]()
将点![]() 代入
代入![]() 得
得![]() ,
,
![]()
将点![]() ,
,![]() 代入
代入![]()
得:![]() ,
,
解得![]()
![]()
所以一次函数的表达式为![]() ,反比例函数的表达式为
,反比例函数的表达式为![]() ;
;
(2)函数![]() 和
和![]() 的图象如图所示,
的图象如图所示,

由图象可得,当![]() 或
或![]() 时,一次函数的值大于反比例函数的值;
时,一次函数的值大于反比例函数的值;
(3)如图,连接PO,QO,设直线与y轴交于点M,
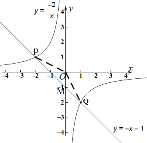
直线![]() 与y轴的交点坐标M(0,-1),即
与y轴的交点坐标M(0,-1),即![]() ,点P到y轴的距离为2,点Q到y轴的距离为1,
,点P到y轴的距离为2,点Q到y轴的距离为1,
![]() ,
,
所以平面直角坐标中原点![]() 与
与![]() 点构成的三角形的面积为
点构成的三角形的面积为![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
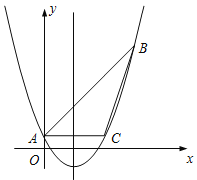
【题目】如图,已知抛物线 y![]() x2 bxc经过△ ABC 的三个顶点,其中点 A(0,1),点 B(9,10),AC∥x 轴,点 P 是直线 AC 下方抛物线上的动点,过点 P 且与 y 轴平行的直线 l 与直线 AB、AC 分别交于点 E、F.
x2 bxc经过△ ABC 的三个顶点,其中点 A(0,1),点 B(9,10),AC∥x 轴,点 P 是直线 AC 下方抛物线上的动点,过点 P 且与 y 轴平行的直线 l 与直线 AB、AC 分别交于点 E、F.
(1)求抛物线的函数表达式;
(2)如图 1,当四边形 AECP 的面积最大时,求点 P 的坐标和四边形 AECP 的最大面积;
(3)如图 2,当点 P 为抛物线的顶点时,在直线 AC 上是否存在点 Q,使得以 C,P,Q 为顶点的三角形与△ ABC 相似?若存在,请直接写出点 Q 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚在实践课上要做一个如图1所示的折扇,折扇扇面的宽度AB是骨柄长OA的![]() ,折扇张开的角度为120°.小刚现要在如图2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料长为24
,折扇张开的角度为120°.小刚现要在如图2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料长为24![]() cm,宽为21cm.小刚经过画图、计算,在矩形布料上裁剪下了最大的扇面,若不计裁剪和粘贴时的损耗,此时扇面的宽度AB为( )
cm,宽为21cm.小刚经过画图、计算,在矩形布料上裁剪下了最大的扇面,若不计裁剪和粘贴时的损耗,此时扇面的宽度AB为( )

A. 21cm B.20 cm C. 19cm D. 18cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的三张形状相同、大小完全相同的方格纸,方格纸中每个小正方形的边长为1,请依次在3个图中画出满足要求的三角形,要求所画的三角形的各顶点必须与方格纸中小正方形的顶点重合.
(1)画一个底边长为4,面积为10的等腰三角形;
(2)画一个面积为10的等腰直角三角形;
(3)画一个一边长为2![]() 且面积为10的等腰三角形.
且面积为10的等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
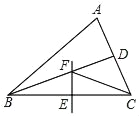
【题目】如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ACF=42°,则∠ABC=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快“秀美荆河水系生态治理工程”进度,污水处理厂决定购买10台污水处理设备.现有A,B两种型号的设备,每台的价格分别为a万元,b万元,每月处理污水量分别为240吨,200吨.已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a,b的值;
(2)厂里预算购买污水处理设备的资金不超过105万元,你认为有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为污水处理厂设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
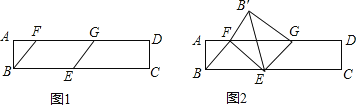
【题目】如图1,矩形ABCD中,AB=![]() ,BC=9,点E在BC边上,BE=4,点F,G在线段AD上运动(点F在点G的左侧),且始终保持FG=BE.
,BC=9,点E在BC边上,BE=4,点F,G在线段AD上运动(点F在点G的左侧),且始终保持FG=BE.
(1)求证:四边形BEGF是平行四边形;
(2)当四边形BEGF是菱形时,求线段DG的长;
(3)将△BEF沿EF折叠得到△B′EF,连结B′G(如图2),当以点B′,G,E,F为顶点的四边形是矩形时,直接写出线段DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
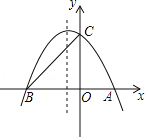
【题目】如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点B的坐标为(﹣3,0),点C的坐标为(0,3),
(1)求抛物线的解析式;(2)在抛物线的对称轴上找一点H,使CH+AH的值最小,求出点H的坐标;
(3)在抛物线上存在点P,满足S△AOP=5,
请求出点P的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com