
【题目】如图,四边形![]() 是矩形,点
是矩形,点![]() 、
、![]() 在坐标轴上,
在坐标轴上, ![]() 是
是![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到的,点
得到的,点![]() 在
在![]() 轴上,直线
轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,线段
,线段![]() ,
,![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积;
的面积;
(3)点![]() 在
在![]() 轴上,平面内是否存在点
轴上,平面内是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形?若存在,请直接写出点
为顶点的四边形是矩形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)可求得![]() 、
、![]() 的坐标,利用待定系数法可求得直线
的坐标,利用待定系数法可求得直线![]() 的解析式;
的解析式;
(2)可求得![]() 点坐标,求出直线
点坐标,求出直线![]() 的解析式,联立直线
的解析式,联立直线![]() 、
、![]() 解析式可求得
解析式可求得![]() 点的横坐标,可求得
点的横坐标,可求得![]() 的面积;
的面积;
(3)当![]() 为直角三角形时,可找到满足条件的点
为直角三角形时,可找到满足条件的点![]() ,分
,分![]() 、
、![]() 和
和![]() 三种情况,分别求得
三种情况,分别求得![]() 点的坐标,可分别求得矩形对角线的交点坐标,再利用中点坐标公式可求得
点的坐标,可分别求得矩形对角线的交点坐标,再利用中点坐标公式可求得![]() 点坐标.
点坐标.
解:(1)![]() ,
,![]() ,
,
![]() ,
,
![]() 是
是![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到的,
得到的,
![]() ,
,![]() ,
,
![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
把![]() 、
、![]() 坐标代入可得
坐标代入可得![]() ,
,
解得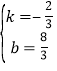 ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ;
;
(2)由(1)可知![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
把点![]() 坐标代入可求得
坐标代入可求得![]() ,
,
![]() 直线
直线![]() 解析式为
解析式为![]() ,
,
令![]() ,解得
,解得![]() ,
,
![]() 点到
点到![]() 轴的距离为
轴的距离为![]() ,
,
又由(1)可得![]() ,
,
![]() ,
,
![]() ;
;
(3)![]() 以点
以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形,
为顶点的四边形是矩形,
![]() 为直角三角形,
为直角三角形,
①当![]() 时,则
时,则![]() 只能在
只能在![]() 轴上,连接
轴上,连接![]() 交
交![]() 于点
于点![]() ,如图1,
,如图1,
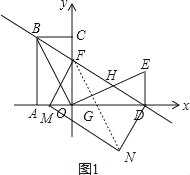
该情况不符合题意.
②当![]() 时,则
时,则![]() 只能在
只能在![]() 轴上,连接
轴上,连接![]() 交
交![]() 于点
于点![]() ,如图2,
,如图2,

则有![]() ,
,
![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ,且
,且![]() ,
,
![]() ,则
,则![]() ,
,
![]() ,
,
设![]() 点坐标为
点坐标为![]() ,则
,则![]() ,
,![]() ,
,
解得![]() ,
,![]() ,此时
,此时![]() ;
;
③当![]() 时,则可知
时,则可知![]() 点为
点为![]() 点,如图,
点,如图,
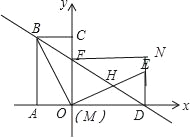
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]() ,
,![]() ,
,
可求得![]() ;
;
综上可知存在满足条件的![]() 点,其坐标为
点,其坐标为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】.如图 1,AB∥CD,直线 EF 交 AB 于点 E,交 CD 于点 F,点 G 在 CD 上,点 P在直线 EF 左侧,且在直线 AB 和 CD 之间,连接 PE,PG.
(1) 求证: ∠EPG=∠AEP+∠PGC;
(2) 连接 EG,若 EG 平分∠PEF,∠AEP+ ∠ PGE=110°,∠PGC=![]() ∠EFC,求∠AEP 的度数.
∠EFC,求∠AEP 的度数.
(3) 如图 2,若 EF 平分∠PEB,∠PGC 的平分线所在的直线与 EF 相交于点 H,则∠EPG 与∠EHG之间的数量关系为 .
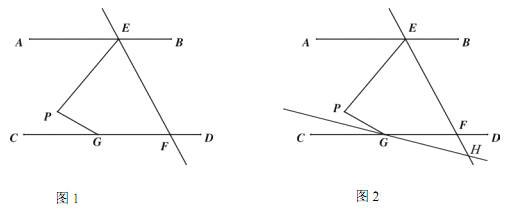
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,问A型节能灯最多可以买多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣2a3b(﹣4a2b)÷6a4b2
(2)![]()
(3)![]()
(4)(2a﹣1)(a﹣4)﹣(a+3)(a﹣4)
(5)(x﹣3y+4)(x+3y﹣4)
(6)(a+2b)(a﹣2b)(a2﹣4b2)
查看答案和解析>>
科目:初中数学 来源: 题型:
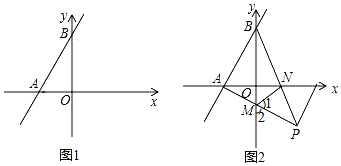
【题目】如图1,在平面直角坐标系中,直线AB分别交x轴、y轴于点![]() 点
点![]() 且a、b满足
且a、b满足![]() .
.
![]() ______;
______;![]() ______.
______.
![]() 点P在直线AB的右侧,且
点P在直线AB的右侧,且![]() ,
,
![]() 若点P在x轴上,则点P的坐标为______;
若点P在x轴上,则点P的坐标为______;
![]() 若
若![]() 为直角三角形,求点P的坐标;
为直角三角形,求点P的坐标;
![]() 如图2,在
如图2,在![]() 的条件下,
的条件下,![]() 且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接
且点P在第四象限,AP与y轴交于点M,BP与x轴交于点N,连接![]() 求证:
求证:![]() 提示:过点P作
提示:过点P作![]() 交x轴于
交x轴于![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为4,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …,按照此规律继续下去,则S10的值为 . 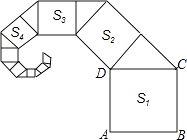
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.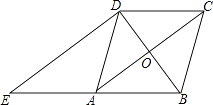
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合与实践课上老师将直尺摆放在三角板上,使直尺与三角板的边分别交于点P、M、N、Q,
(1)如图①所示.当∠CNG=42°,求∠HMC 的度数.(写出证明过程)
(2)将直尺向下平移至图 2 位置,使直尺的边缘通过点 C,交 AB 于点 P,直尺另一侧与三角形交于 N、Q 两点。请直接写出∠PQF、∠A、∠ACE 之间的关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com