
如图1,已知四边形OABC中的三个顶点坐标为O(0,0),A(0,n),C(m,0).动点P从点O出发依次沿线段OA,AB,BC向点C移动,设移动路程为z,△OPC的面积S随着z的变化而变化的图象如图2所示.m,n是常数,m>1,n>0.

(1)请你确定n的值和点B的坐标;
(2)当动点P是经过点O,C的抛物线y=ax2+bx+c的顶点,且在双曲线y=![]() 上时,求这时四边形OABC的面积.
上时,求这时四边形OABC的面积.
|
解:(1)从图中可知,当P从O向A运动时,△POC的面积S= 同理,AB=1,故点B的坐标是(1,2) (2分) (2)解法一: ∵抛物线y=ax ∴抛物线为y=ax 如图1,设经过点O,C,P的抛物线为l
当P在OA上运动时,O,P都在y轴上,这时P,O,C三点不可能同在一条抛物线上, ∴这时抛物线l不存在,故不存在m的值 ① 当点P与C重合时,双曲线y= 故也不存在m的值 ② (5分) (说明:①②任做对一处评1分,两处全对也只评一分) 当P在AB上运动时,即当0<x 抛物线l的顶点为P( ∵P在双曲线y= 容易求得直线BC的解析式是: 当P在BC上运动,设P的坐标为(x 故得y ∵1<x 于是, 解得 与题意2<x 故由①②③④,满足条件的只有一个值: 这时四边形OABC的面积= (2)解法二: ∵抛物线y=ax ∴c=0,b=-am,(3分) ∴抛物线为y=ax ∵m>1,∴ ∴P不在边OA上且不与C重合 (5分) ∵P在双曲线y= ①当1<m≤2时,
M,N为垂足,此时点P在线段AB上,且纵坐标为2, ∴- 而a=- ②当m≥2时,
此时点P在线段CB上,易证Rt△BMC∽Rt△PNC, ∴BM∶PN=MC∶NC,即:2∶PN=(m-1)∶ 而P的纵坐标为- 而a=- 化简得:5m2-22m+22=0解得:m= 但m≥2,所以m= 取m= 由以上,这时四边形OABC的面积为: |


科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
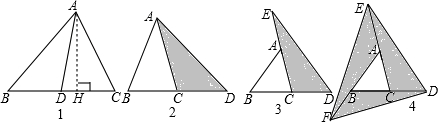
查看答案和解析>>
科目:初中数学 来源: 题型:
| FH |
| AB |
| FG |
| BG |
| FH |
| AB |
| FG |
| BG |
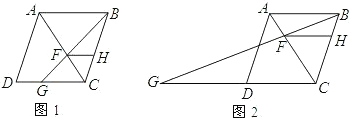
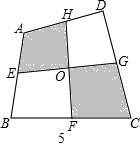
查看答案和解析>>
科目:初中数学 来源: 题型:
| k | x |
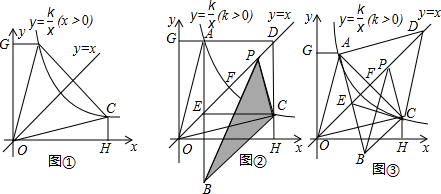
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com