
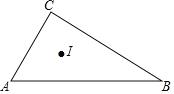
【题目】已知∠ACB=90°,∠CAB=a,且sina=![]() ,I为内心,则△ABC的内切圆半径r与△BIC的外接圆半径R之比为( )
,I为内心,则△ABC的内切圆半径r与△BIC的外接圆半径R之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
作ID⊥AC于D,△CIB外接圆的圆心为O,作OE⊥BC于E,交直线ID于F,连接OC,求出直角三角形ABC的内切圆半径,由勾股定理得出方程,求出△BIC的外接圆半径R,即可得出结果.
作ID⊥AC于D,△CIB外接圆的圆心为O,作OE⊥BC于E,交直线ID于F,连接OC,如图所示:
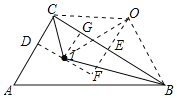
∵∠ACB=90°,∠CAB=a,且sina=![]() ,
,
设AB=5b,BC=4b,则AC=3b,
∴△ABC的内切圆的半径![]() ,
,
∵I是Rt△ABC的内心,
∴CD=ID=CG=b,
∵OE⊥BC,
∴CE=BE=![]() BC=2b,
BC=2b,
易得四边形CDFE为矩形,
∴EF=CD=b,DF=CE=2b,
∴IF=2b-b=b,
设OE=x,⊙O的半径为R,则OF=x+b,OC=OI=R,
在Rt△OCE中,x![]() +(2b)
+(2b)![]() =R
=R![]() ①,
①,
在Rt△OIF中,(x+b)![]() +b
+b![]() =R
=R![]() ②,
②,
②-①得:2ax=2a![]() ,解得x=a,
,解得x=a,
∴![]()
∴△ABC的内切圆半径r与△BIC的外接圆半径R之比=![]() ;
;
故选:B.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
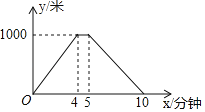
【题目】在一段长为1000的笔直道路AB上,甲、乙两名运动员均从A点出发进行往返跑训练.已知乙比甲先出发30秒钟,甲距A点的距离y(米)与其出发的时间x(分钟)的函数图象如图所示,乙的速度是150米分钟,且当乙到达B点后立即按原速返回.
(1)当x为何值时,两人第一次相遇?
(2)当两人第二次相遇时,求甲的总路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
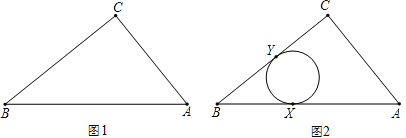
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标平面内的三个点![]() 、
、![]() 、
、![]() .
.
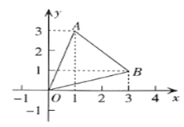
(1)比较![]() 点到
点到![]() 轴的距离与
轴的距离与![]() 点到
点到![]() 轴距离的大小;
轴距离的大小;
(2)平移![]() 至
至![]() ,当点
,当点![]() 和点
和点![]() 重合时,求点
重合时,求点![]() 的坐标;
的坐标;
(3)平移![]() 至
至![]() ,需要至少向下平移超过 单位,并且至少向左平移 个单位,才能使
,需要至少向下平移超过 单位,并且至少向左平移 个单位,才能使![]() 位于第三象限.
位于第三象限.
查看答案和解析>>
科目:初中数学 来源: 题型:
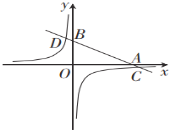
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象分别交x轴、y轴于A、B两点,与反比例函数
的图象分别交x轴、y轴于A、B两点,与反比例函数![]() 的图象交于C、D两点.已知点C的坐标是(6,-1),D(n,3).
的图象交于C、D两点.已知点C的坐标是(6,-1),D(n,3).
(1)求m的值和点D的坐标.
(2)求![]() 的值.
的值.
(3)根据图象直接写出:当x为何值时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产一种健身产品在市场上很受欢迎,该公司每年的年产量为6万件,每年可在国内和国外两个市场全部销售,若在国内销售,平均每件产品的利润y1(元)与国内销售量x(万件)的函数关系式为![]() ,若在国外销售,平均每件产品的利润为71元.
,若在国外销售,平均每件产品的利润为71元.
(1)求该公司每年的国内和国外销售的总利润w(万元)与国内销售量x(万件)的函数关系式,并指出x的取值范围.
(2)该公司每年的国内国外销售量各为多少时,可使公司每年的总利润最大?最大值是多少?
(3)该公司计划在国外销售不低于5万件,并从国内销售的每件产品中捐出2m(5≤m≤10)元给希望工程,从国外销售的每件产品中捐出m元给希望工程,若这时国内国外销售的最大总利润为393万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
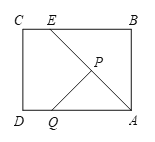
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 为边
为边![]() 上一点,
上一点,![]() ,连接
,连接![]() .动点
.动点![]() 从点
从点![]() 同时出发,点
同时出发,点![]() 以
以![]() 的速度沿
的速度沿![]() 向终点
向终点![]() 运动;点
运动;点![]() 以
以![]() 的速度沿折线
的速度沿折线![]() 向终点
向终点![]() 运动.设点
运动.设点![]() 运动的时间为
运动的时间为![]() ,在运动过程中,点
,在运动过程中,点![]() ,点
,点![]() 经过的路线与线段
经过的路线与线段![]() 围成的图形面积为
围成的图形面积为![]() .
.
⑴![]() ________
________![]() ,
,![]() ________°;
________°;
⑵求![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
⑶当![]() 时,直接写出
时,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动,几秒种后△DPQ的面积为31cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
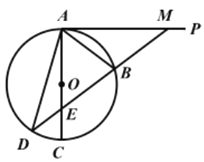
【题目】如图,AC是⊙O的一条弦,AP是⊙O的切线。作BM=AB并与AP交于点M,延长MB交AC于点E,交⊙O于点D,连接AD.
(1)求证:AB=BE;
(2)若⊙O的半径R=5,AB=6,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com