
【题目】如图,边长为![]() 的正方形
的正方形![]() 中,
中,![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,则
,则![]() 的长为________.
的长为________.
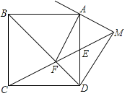
【答案】![]()
【解析】
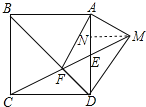
作MN⊥AD,先证明MA=ME,进而求出AN=NE=1,利用MN∥CD得:![]() ,
,
求出MN,在RT△MND中利用勾股定理即可求出DM.
作MN⊥AD垂足为N.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABF=∠CBF,BC∥AD,∠BAD=∠CDA=90°,
∵BF=BF,
∴△BFA≌△BFC,
∴∠BAF=∠BCF=∠CED=∠AEM,
∵∠MAF=∠BAD=90°,
∴∠BAF=∠MAE,
∴∠MAE=∠AEM,
∴MA=ME
∵AE=ED=![]() AD=2,
AD=2,
∴AN=NE=![]() AE=1,
AE=1,
∵∠MNE=∠CDE=90°,
∴MN∥CD,
∴△MNE∽△CDE,
∴![]() =
=![]() ,
,
∵CD=4,
∴MN=2,
在RT△MND中,∵MN=2,DN=3,
∴DM=![]() =
=![]() =
=![]() ,
,
故答案为:![]()


科目:初中数学 来源: 题型:
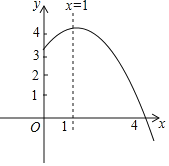
【题目】抛物线![]() 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() 下列结论中:
下列结论中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有两个不相等的实数根;
有两个不相等的实数根;![]() 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为![]() ;
;![]() 若点
若点![]() 在该抛物线上,则
在该抛物线上,则![]() .
.
其中正确的有![]()
![]()
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+x+2
x2+x+2![]() 与x轴交于A,B两点,交y轴于点C,点C关于抛物线对称轴对称的点为D.
与x轴交于A,B两点,交y轴于点C,点C关于抛物线对称轴对称的点为D.
(1)求点D的坐标及直线AD的解析式;
(2)如图1,连接CD、AD、BD,点M为线段CD上一动点,过M作MN∥BD交线段AD于N点,点P是y轴上的动点,当△CMN的面积最大时,求△MPN的周长取得最小值时点P的坐标;
(3)如图2,线段AE在第一象限内交BD于点E,其中tan∠EAB=![]() ,将抛物线向右水平移动,点A平移后的对应点为点G;将△ABD绕点B逆时针旋转,旋转后的三角形纪为△A1BD1,若射线BD1与线段AE的交点为F,连接FG.若线段FG把△ABF分成△AFG和△BFG两个三角形,是否存在点G,使得△AFG是直角三角形且△BFG是等腰三角形?若存在,请直接写出点G的坐标;若不存在,请说明理由.
,将抛物线向右水平移动,点A平移后的对应点为点G;将△ABD绕点B逆时针旋转,旋转后的三角形纪为△A1BD1,若射线BD1与线段AE的交点为F,连接FG.若线段FG把△ABF分成△AFG和△BFG两个三角形,是否存在点G,使得△AFG是直角三角形且△BFG是等腰三角形?若存在,请直接写出点G的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并回答问题.事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方,这个结论就是著名的勾股定理.请利用这个结论,完成下面活动:
![]() 一个直角三角形的两条直角边分别为
一个直角三角形的两条直角边分别为![]() ,那么这个直角三角形斜边长为____;
,那么这个直角三角形斜边长为____;
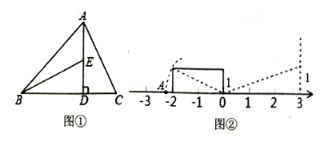
![]() 如图①,
如图①,![]() 于
于![]() ,求
,求![]() 的长度;
的长度;
![]() 如图②,点
如图②,点![]() 在数轴上表示的数是____请用类似的方法在图2数轴上画出表示数
在数轴上表示的数是____请用类似的方法在图2数轴上画出表示数![]() 的
的![]() 点(保留痕迹).
点(保留痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法“①凡正方形都相似;②凡等腰三角形都相似;③凡等腰直角三角形都相似;④直角三角形斜边上的中线与斜边的比为![]() ;⑤两个相似多边形的面积比为
;⑤两个相似多边形的面积比为![]() ,则周长的比为
,则周长的比为![]() .”中,正确的个数有( )个
.”中,正确的个数有( )个
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,点
,点![]() 将线段
将线段![]() 分成两部分,如果
分成两部分,如果![]() ,那么称点
,那么称点![]() 为线段
为线段![]() 的黄金分割点.
的黄金分割点.
![]() 某研究小组在进行课题学习时,类似地给出“黄金分割线”的定义:直线
某研究小组在进行课题学习时,类似地给出“黄金分割线”的定义:直线![]() 将一个面积为
将一个面积为![]() 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为![]() ,
,![]() ,如果
,如果![]() ,那么称直线
,那么称直线![]() 为该图形的黄金分割线.(如图
为该图形的黄金分割线.(如图![]() )
)
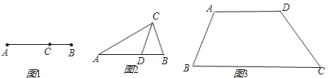
问题.试在图![]() 的梯形中画出至少五条黄金分割线,并说明理由.
的梯形中画出至少五条黄金分割线,并说明理由.
![]() 类似“黄金分割线”得“黄金分割面”定义:截面
类似“黄金分割线”得“黄金分割面”定义:截面![]() 将一个体积为
将一个体积为![]() 的图形分成体积为V1
的图形分成体积为V1
、![]() 的两个图形,且
的两个图形,且![]() ,则称直线
,则称直线![]() 为该图形的黄金分割面.
为该图形的黄金分割面.
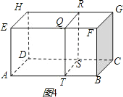
问题:如图![]() ,长方体
,长方体![]() 中,
中,![]() 是线段
是线段![]() 上的黄金分割点,证明经过
上的黄金分割点,证明经过![]() 点且平行于平面
点且平行于平面![]() 的截面
的截面![]() 是长方体的黄金分割面.
是长方体的黄金分割面.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=10,cosB=![]() ,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
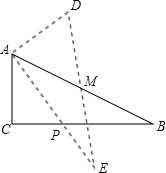
查看答案和解析>>
科目:初中数学 来源: 题型:
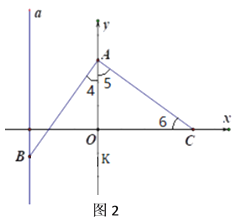
【题目】已知,在平面直角坐标系中,点![]() ,
,![]() ,过
,过![]() 点作直线
点作直线![]() 与
与![]() 轴互相垂直,
轴互相垂直,![]() 为
为![]() 轴上的一个动点,且
轴上的一个动点,且![]() .
.
(1)如图1,若点![]() 是第二象限内的一个点,且
是第二象限内的一个点,且![]() 时,求点
时,求点![]() 的坐标;(用
的坐标;(用![]() 的代数式表示)
的代数式表示)
(2)如图2,若点![]() 是第三象限内的一个点,设
是第三象限内的一个点,设![]() 点的坐标
点的坐标![]() ,求
,求![]() 的取值范围:
的取值范围:
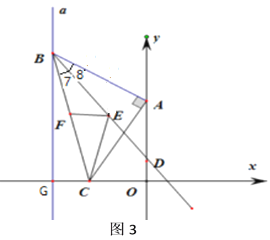
(3)如图3,连接![]() ,作
,作![]() 的平分线
的平分线![]() ,点
,点![]() 、
、![]() 分别是射线
分别是射线![]() 与边
与边![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() ,当
,当![]() 时,试求
时,试求![]() 的最小值.
的最小值.
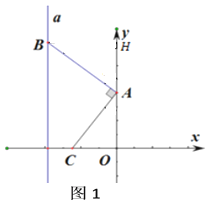
查看答案和解析>>
科目:初中数学 来源: 题型:
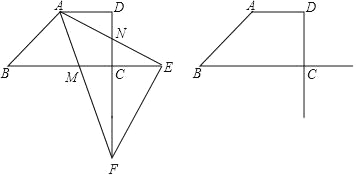
【题目】如图,梯形ABCD中,AD∥BC,DC⊥BC,且∠B=45°,AD=DC=1,点M为边BC上一动点,联结AM并延长交射线DC于点F,作∠FAE=45°交射线BC于点E、交边DCN于点N,联结EF.
(1)当CM:CB=1:4时,求CF的长.
(2)设CM=x,CE=y,求y关于x的函数关系式,并写出定义域.
(3)当△ABM∽△EFN时,求CM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com