
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�OΪ����ԭ�㣬������y��a��x+3����x��1����a��0����x�ύ��A��B���㣨��A�ڵ�B����ࣩ��
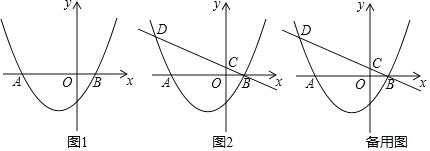
��1�����A���B�����ꣻ
��2����a��![]() ����M����������һ���㣬�������MAO������45�������M�ĺ�����m��ȡֵ��Χ��
����M����������һ���㣬�������MAO������45�������M�ĺ�����m��ȡֵ��Χ��
��3��������B��ֱ��l��y��kx+b��y�������ύ�ڵ�C���������ߵ���һ������Ϊ��D����CD��4BC������P�������߶Գ����ϣ���Q���������ϣ��Ե�B��D��P��QΪ������ı����ܷ��Ϊ���Σ����ܣ������P�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��A����3��0����B��1��0������2��M��4��7������2��m��4����3����P������ΪP����1��4����1��![]() ����
����
��������
��1��y��a��x+3����x��1��,��y��0,��x��1��3,�������;
��2���֡�MAO=45��,��M��AO=45���������,�ֱ���⼴��;
��3���ֵ�BD�Ǿ��εı�, BD�Ǿ��εı��������,�ֱ���⼴�ɣ�
��1��y��a��x+3����x��1��,��y��0,��x��1��3,
�ʵ�A��B������ֱ�Ϊ������3��0��,��1��0��;
��2�������ߵı���ʽΪ:y��![]() ��x+3����x��1����,
��x+3����x��1����,
����MAO��45��ʱ,��ͼ��ʾ,��ֱ��AM�ı���ʽΪ:y��x��,
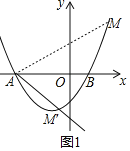
�����٢ڲ����:m��x��4��3����ȥ��3��,�ʵ�M��4,7��;
�ڡ�M��AO��45��ʱ,
ͬ���ɵ�:��M����2,��1��;
��:��2��m��4;
��3���ٵ�BD�Ǿ��εĶԽ���ʱ,��ͼ2��ʾ,
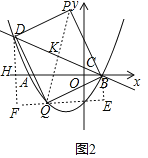
����Q��x���ƽ����EF,����B��BE��EF,����D��DF��EF,
�����ߵı���ʽΪ:y��ax2+2ax��3a,�����ĶԳ���Ϊ:x��1,
�����ߵ�A��B������ֱ�Ϊ:����3,0������1��0��,���P�ĺ�����Ϊ:1,OB��1,
��CD��4BC,���D�ĺ�����Ϊ����4,�ʵ�D����4,5a��,��HD��5a,
�߶�BD���е�K�ĺ�����Ϊ:![]() ,���Q�ĺ�����Ϊ:��2,
,���Q�ĺ�����Ϊ:��2,
���Q����2,��3a��,��HF��BE��3a,
�ߡ�DQF+��BQE��90��,��BQE+��QBE��90��,
���QBE����DQF,
���DFQ�ס�QEB,��![]() ,
,![]() ,���:a��
,���:a��![]() ����ȥ��ֵ��,
����ȥ��ֵ��,
ͬ����PGB�ա�DFQ��AAS��,
��PG��DF��8a��4,�ʵ�P����1,4��;
����ͼ3,��BD�Ǿ��εı�ʱ,
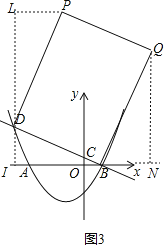
��DI��x��,QN��x��,����P��PL��DI�ڵ�L,
ͬ����PLD�ա�BNQ��AAS��,
��BN��PL��3,
���Q�ĺ�����Ϊ4,���Q��4,21a��,
��QN��DL��21a,ͬ����PLD�ס�DIB,
��![]() ,��
,��![]() ,���:a��
,���:a��![]() ����ȥ��ֵ����
����ȥ��ֵ����
LI��26a��![]() ,�ʵ�P����1,
,�ʵ�P����1, ![]() ��;
��;
����,��P������Ϊ:P����1,4����1, ![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ܵ�ѧУʳ��������A��B������ǰ���Ŷӵ���һ����(��Ϊa�ˣ�a��8������վ��A���ڶ���ĺ��棬����2���ӣ�������A����ÿ������4�����˷��뿪���飬B����ÿ������6�����˷��뿪���飬��B���ڶ������ÿ��������5�ˣ�
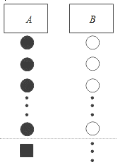
��1����ʱ����С�ܼ�����A�����Ŷӣ��������ﴰ��������ʱ���Ƕ��٣����ú�a�Ĵ���ʽ��ʾ��
��2����ʱ����С��Ѹ�ٴ�A���ڶ���ת�Ƶ�B���ں��������Ŷӣ��ҵ���B����������ʱ��ȼ�����A�����Ŷӵ���A����������ʱ���٣���a��ȡֵ��Χ�����������������أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
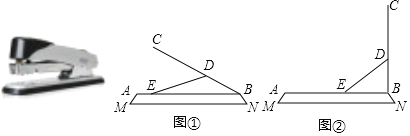
����Ŀ�����ճ����������Ǿ�����ʹ�õ����������ͼMN��װ�����ĵ�����AB��װ�������а�ABʼ�������ƽ�У����Ӹ�DE��D��̶�����E��A��B��������ѹ��BC����ת��B��ת����֪���Ӹ�BC�ij���Ϊ20cm��BD=![]() cm��ѹ�����а�ij�����ȣ�
cm��ѹ�����а�ij�����ȣ�
��1�����а���ѹ���ļнǡ�ABC=30��ʱ����ͼ�ٵ�E��A�㻬����2cm�������Ӹ�DE�ij��ȣ�
��2����ѹ��BC�ӣ�1���е�λ����ת���������ֱ����ͼ�ڣ�����������У���E�����ľ��룮������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() ��ͼ����һ�κ���
��ͼ����һ�κ���![]() ��ͼ����M��1��3����N���㣬��N�ĺ�����Ϊ��3��
��ͼ����M��1��3����N���㣬��N�ĺ�����Ϊ��3��

��1������ͼ����Ϣ�ɵù���x�ķ���![]() �Ľ�Ϊ ��
�Ľ�Ϊ ��
��2����һ�κ����Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��![]() ��
��![]() ��Ϊ����ֱ�������Σ�
��Ϊ����ֱ�������Σ�![]() ������
������![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ������һֱ���ϣ�
������һֱ���ϣ�![]() ��
��![]() ��
��
��1����֤��![]() ��
��
��2�����߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
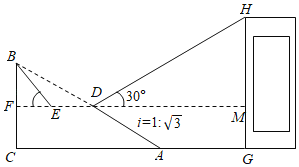
����Ŀ����ͼ����ӢѧУǰ����һб��AB��60�ף��¶�i��1��![]() ��BC��AC���ּƻ���б���е�D����ȥ�������壨����Ӱ��ʾ������һ��ƽ����ˮƽ��CA��ƽ̨DE��һ���µ�б��BE��
��BC��AC���ּƻ���б���е�D����ȥ�������壨����Ӱ��ʾ������һ��ƽ����ˮƽ��CA��ƽ̨DE��һ���µ�б��BE��
��1��������б��BE���½ǣ�����BEF��������45�㣬��ƽ��DE��Ƕ����ף�
��2��ѧУ��ѧ¥GH�����½�A��27��Զ����AG��27�ף���С����D���ý�ѧ¥����H�����ǣ�����HDM��Ϊ30�㣮��B��C��A��G��H��ͬһ��ƽ���ϣ���C��A��G��ͬһ��ֱ���ϣ���HG��CG���ʣ���ѧ¥GH��Ϊ�����ף��������ȷ��0.1�ף��ο�����![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �Ļ���ԽҰ���У�������ѡ�ֵ��г�
�Ļ���ԽҰ���У�������ѡ�ֵ��г�![]() (��λ��
(��λ��![]() )��ʱ��
)��ʱ��![]() (��λ��
(��λ��![]() )�仯��ͼ����ͼ��ʾ������ͼ���ṩ����Ϣ������˵���У�������ǣ�( )
)�仯��ͼ����ͼ��ʾ������ͼ���ṩ����Ϣ������˵���У�������ǣ�( )
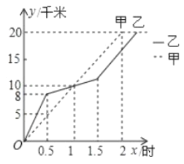
A.������1Сʱ�������г̾�Ϊ![]() ��B.������1.5Сʱ�����г̱��Ҷ�
��B.������1.5Сʱ�����г̱��Ҷ�![]() ��
��
C.��������ǰ�����ٶ�С���ҵ��ٶȣ�D.�ױ����ȵ����յ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
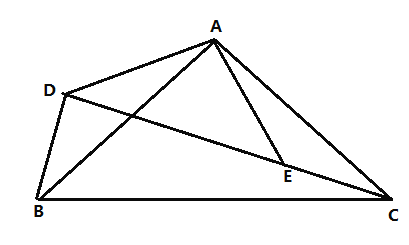
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��DΪ��BC��һ�㣬��AB��BDΪ�ڱ���ABDE������AD��EC��
��1����֤����ADC�ա�ECD��
��2����BD=CD����֤���ı���ADCE�Ǿ��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
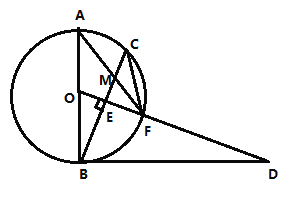
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() Ϊ
Ϊ![]() ��һ�㣬
��һ�㣬![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬��
�ӳ�����һ�㣬��![]() ��
��
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2����֤��![]() ��
��
��3����![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com