
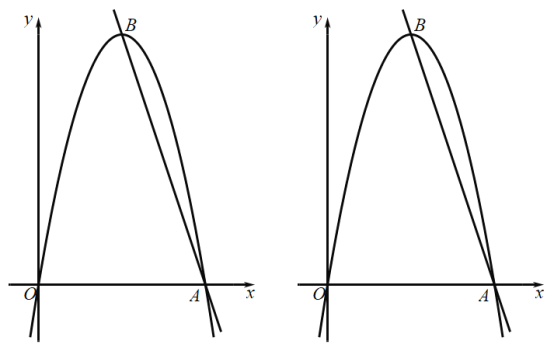
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的正半轴交于点A,抛物线的顶点为B,直线
轴的正半轴交于点A,抛物线的顶点为B,直线![]() 经过A,B两点,且
经过A,B两点,且![]() .
.
(1)求抛物线的解析式
(2)点P在第一象限内对称轴右侧的抛物线上,其横坐标为![]() ,连接OP,交对称轴于点C,过点C作
,连接OP,交对称轴于点C,过点C作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,连接
,连接![]() ,设线段
,设线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,交
,交![]() 于点F,点G是BE的中点,过点G作
于点F,点G是BE的中点,过点G作![]() 轴,交
轴,交![]() 的延长线于点
的延长线于点![]() ,当
,当![]() 且
且![]() 时,求点
时,求点![]() 的坐标;
的坐标;
【答案】(1)抛物线解析式为![]() ;(2)
;(2)![]() ,自变量的取值范围是
,自变量的取值范围是![]() ;(3)
;(3)![]() ,点
,点![]() 的坐标为
的坐标为![]()
【解析】
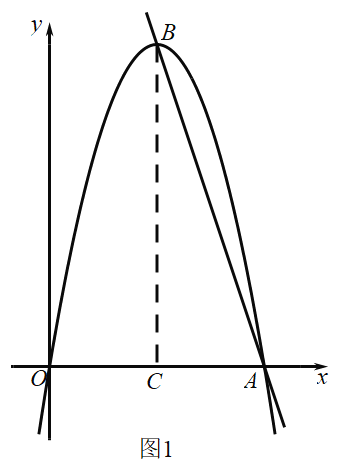
(1)过点B作BC⊥OA垂足为C.令y=0可求得点A的坐标,由抛物线的对称性可得到AC=3,然后依据锐角三角形函数的定义可得到BC的长,从而得到点B的坐标;将点A和点B的坐标代入抛物线的解析式,可求得a、b的值,于是可求得抛物线的解析式;
(2)先求得直线AB的解析式,设P的坐标为(t,-t2+6t),可求得直线OP的解析式为y=(-t+6)x,接下来,求得点C的纵坐标,从而得到D点的纵坐标为-3t+18.接下来将点D点的纵坐标代入直线AB的解析式可求得点D的横坐标,然后根据P点和D点的横坐标相同,可至PD的长等于P、D两点的纵坐标之差;
(3)延长PQ交y轴于点H,过点P作PM∥x轴.先证明∠PMH=∠PMO,于是可证明△PHM≌△POM,由全等三角形的性质可得到HM=OM,设P(a,-a2+6a),则H(0,-2a2+12a).接下来,求得PH的解析式(用含a的式子表示);于是可求得点E的纵坐标为,由中点坐标公式可求得F的坐标(用含a的式子表示),将F的坐标代入直线AB的解析式可求得a的值,于是可求得点P的坐标、PH的解析式、点E的坐标,然后依据中点坐标公式可求得点G的坐标,从而得到点Q的纵坐标,然后将点Q的纵坐标代入PH的解析式可求得点Q的横坐标,于是可求得点Q的坐标,最后将点Q的坐标代入抛物线的解析式即可作出判断.
(1)如图1所示,过点B作![]() ,
,
令![]() 则
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
因为抛物线经过点![]() ,且B为顶点,
,且B为顶点,
所以![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,解得
,解得![]() ,
,
所以抛物线解析式为![]() .
.
(2)如图2所示,
设直线AB解析式为![]() ,
,
则![]() ,
,
解得![]() ,
,
所以直线解析式为![]() ,
,
设点P的坐标为![]() ,OP的解析式为
,OP的解析式为![]() ,
,
![]() ,
,
将![]() 代入解析式得
代入解析式得![]() ,
,
![]() ,
,
![]() 轴,
轴,![]() 的纵坐标为
的纵坐标为![]() ,
,
将![]() 代入直线AB的解析式得:
代入直线AB的解析式得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 轴,
轴,![]() ,
,
自变量的取值范围是![]() .
.
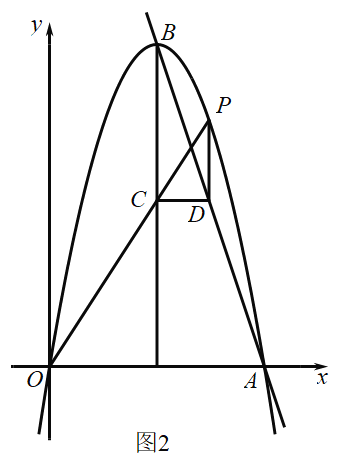
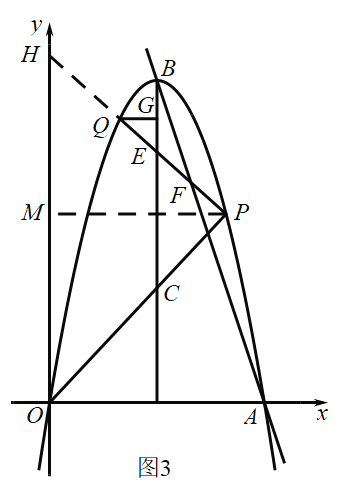
如图3所示:延长![]() 交
交![]() 轴于
轴于![]() 点,过点P作
点,过点P作![]() 轴,
轴,
![]() 轴,
轴,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 轴,
轴,
![]() ,
,
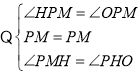 ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
设PH的解析式为![]() ,
,
将点P的坐标代入得:![]() ,
,
解得![]() ,
,
所以直线PH的解析式为![]() ,
,
将![]() 代入得解析式为
代入得解析式为![]() ,
,
所以点E的纵坐标为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
将![]() 代入AB的解析式得:
代入AB的解析式得:![]() ,
,
![]() ,
,
整理得:![]() ,
,
解得![]() 或
或![]() (舍去)
(舍去)
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
所以直线PH的解析式为![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 轴,所以
轴,所以![]() 的纵坐标为8,
的纵坐标为8,
将![]() 代入
代入![]() ,得
,得![]() ,
,
解得![]() ,
,
所以点![]() 的坐标为
的坐标为![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与y轴交于点
与y轴交于点![]() .
.
(1)求c的值;
(2)当![]() 时,求抛物线顶点的坐标;
时,求抛物线顶点的坐标;
(3)已知点![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有两个公共点,结合函数图象,求a的取值范围.
有两个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.

(1)、如图a,求证:△BCP≌△DCQ;
(2)、如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推动阳光体育运动的广泛开展,引导学生走向大自然,走到阳光下积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如图所示两个统计图,请根据相关信息,解答下列问题:
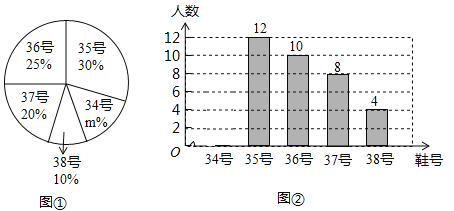
(1)求本次抽样调查的学生人数
(2)通过计算补全条形统计图和扇形统计图;
(3)若学生计划购买200双运动鞋,建议购买35号运动鞋约多少双?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数的图象过点(4,-5)和(0,3),且与x轴交于点M(-1,0)和N,
(1)求此二次函数的解析式;
(2)如果这二次函数的图像的顶点为点P,点O是坐标原点,求△OPN的面积.
(3)如果点R与点P关于x轴对称,判定以M、N、P、R为顶点的四边形的边之间的位置与度量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
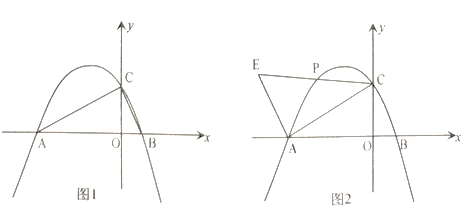
【题目】如图1,已知开口向下的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 不小于
不小于![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)求系数![]() 的取值范围;
的取值范围;
请你根据自身能力从![]() 或(4)小题中任选-题作答.
或(4)小题中任选-题作答.
(3)如图2,当![]() 时,
时,![]() 为直线
为直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 试探究是否存在点
试探究是否存在点![]() ,使得
,使得![]() 的某一个角等于
的某一个角等于![]() 的
的![]() 倍?若存在,求点
倍?若存在,求点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
(4)如图2,当![]() 时,
时,![]() 为直线
为直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 抛物线的对称轴与
抛物线的对称轴与![]() 轴交于点
轴交于点![]() 连接
连接![]() 试探究是否存在点
试探究是否存在点![]() 使得
使得![]() 与
与![]() 相似?若存在,求点
相似?若存在,求点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师将自己2019年10月至2020年5月的通话时长(单位:分钟)的有关数据整理如下:
①2019年10月至2020年3月通话时长统计表
时间 | 10月 | 11月 | 12月 | 1月 | 2月 | 3月 |
时长(单位:分钟) | 520 | 530 | 550 | 610 | 650 | 660 |
②2020年4月与2020年5月,这两个月通话时长的总和为1100分钟根据以上信息,推断张老师这八个月的通话时长的中位数可能的最大值为( )
A.550B.580C.610D.630
查看答案和解析>>
科目:初中数学 来源: 题型:
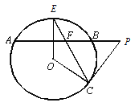
【题目】如图,AB 是⊙O 的弦,半径OE⊥ AB ,P 为 AB 的延长线上一点,PC 与⊙O相切于点 C,连结 CE,交 AB 于点 F,连结 OC.
(1)求证:PC=PF.
(2)连接 BE,若∠CEB=30°,半径为 8,tan P ![]() ,求 FB 的长.
,求 FB 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com