
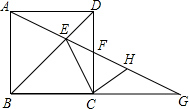
 如图所示,在正方形ABCD中,点F在CD边上,射线AF交BD于点E,交BC的延长线于点G.求证:
如图所示,在正方形ABCD中,点F在CD边上,射线AF交BD于点E,交BC的延长线于点G.求证: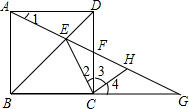 (1)证明:∵四边形ABCD是正方形,
(1)证明:∵四边形ABCD是正方形,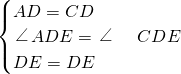 ,
, FG=GH,
FG=GH,

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•凤阳县模拟)如图所示,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连结AE,CE.延长CE到F,连结BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为
(2013•凤阳县模拟)如图所示,在正方形ABCD的对角线上取点E,使得∠BAE=15°,连结AE,CE.延长CE到F,连结BF,使得BC=BF.若AB=1,则下列结论:①AE=CE;②F到BC的距离为
| ||
| 2 |
| 1 |
| 4 |
| ||
| 8 |
| ||
| 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
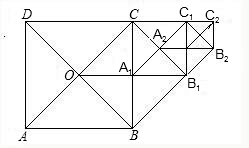
 如图所示,在正方形网格上有一个△ABC.
如图所示,在正方形网格上有一个△ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com