
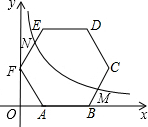
 如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )
如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )| A. | ($\frac{7}{4}\sqrt{3},4$) | B. | ($\frac{7}{4},4\sqrt{3}$) | C. | (2$\sqrt{2}-1,2\sqrt{6}+\sqrt{3}$) | D. | (2$\sqrt{2}+1,2\sqrt{6}-\sqrt{3}$) |
分析 利用正六边形的性质结合锐角三角函数关系得出M,F,E点的坐标,再利用直线与反比例函数交点求法得出N点坐标.
解答 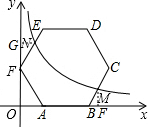 解:过点M作MF⊥x轴于点F,过点N作NG⊥y轴于点G,
解:过点M作MF⊥x轴于点F,过点N作NG⊥y轴于点G,
∵边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,
∴BM=2,∠GFN=30°,∠BMF=60°,∠OFA=30°,
∴GN=$\frac{1}{2}$FN,BF=$\frac{1}{2}$BM=1,AO=$\frac{1}{2}$AF=2,MF=$\sqrt{3}$,FO=2$\sqrt{3}$,E(2,4$\sqrt{3}$),F(0,2$\sqrt{3}$),
∴M(7,$\sqrt{3}$),
∴k=7$\sqrt{3}$,
则反比例函数解析式为:y=$\frac{7\sqrt{3}}{x}$,
设直线EF的解析式为:y=ax+b,
则$\left\{\begin{array}{l}{b=2\sqrt{3}}\\{2a+b=4\sqrt{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\sqrt{3}}\\{b=2\sqrt{3}}\end{array}\right.$,
∴直线EF的解析式为:y=$\sqrt{3}$x+2$\sqrt{3}$,
故$\sqrt{3}$x+2$\sqrt{3}$=$\frac{7\sqrt{3}}{x}$,
解得:x1=-1+2$\sqrt{2}$,x2=-1-2$\sqrt{2}$(不合题意舍去),
∴N点横坐标为:-1+2$\sqrt{2}$,
∴N点纵坐标为:y=$\frac{7\sqrt{3}}{-1+2\sqrt{2}}$=2$\sqrt{6}$+$\sqrt{3}$.
故选:C.
点评 此题主要考查了正多边形与圆以及反比例函数与一次函数应用,正确得出M点坐标是解题关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
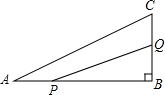 如图,在△ABC中,∠B=90°,AB=6cm,BC=3cm,点P以1cm/s的速度从点A开始沿边AB向点B移动,点Q以2cm/s的速度从点B开始沿边BC向点C移动,如果点P、Q分别从点A、B同时出发,多少时间后P、Q之间的距离等于4$\sqrt{2}$cm?
如图,在△ABC中,∠B=90°,AB=6cm,BC=3cm,点P以1cm/s的速度从点A开始沿边AB向点B移动,点Q以2cm/s的速度从点B开始沿边BC向点C移动,如果点P、Q分别从点A、B同时出发,多少时间后P、Q之间的距离等于4$\sqrt{2}$cm?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知矩形OABC在直角坐标系中的位置如图,点B的坐标为(8,4).把矩形沿对角线OB折叠,使点A落在点D上,OD交CB于点E,过点E的双曲线y=$\frac{k}{x}$(x>0)交AB于F,求AF的长.
已知矩形OABC在直角坐标系中的位置如图,点B的坐标为(8,4).把矩形沿对角线OB折叠,使点A落在点D上,OD交CB于点E,过点E的双曲线y=$\frac{k}{x}$(x>0)交AB于F,求AF的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-1=(x-1)2 | B. | x2+2x-1=(x+1)2 | C. | 2x2-2=2(x+1)(x-1) | D. | x2-6x+9=x(x-6)+9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13 | B. | 14 | C. | 15 | D. | 28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com