
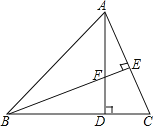
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 于点E,
于点E,![]() 于点D,BE与AD相交于F.
于点D,BE与AD相交于F.
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,求AF的长.
,求AF的长.
【答案】(1)证明见解析(2)AF=3![]()
【解析】
(1)根据等腰三角形腰长相等性质可得AD=BD,即可求证△BDF≌△ACD,即可解答;
(2)连接CF,根据全等三角形的性质得到DF=DC,得到△DFC是等腰直角三角形.推出AE=EC,BE是AC的垂直平分线.于是得到结论.
解:(1)AD⊥BD,∠BAD=45°,
∴AD=BD,
∵∠BFD=∠AFE,∠AFE+∠CAD=90°,∠CAD+∠ACD=90°,
∴∠BFD=∠ACD,
在△BDF和△ACD中,
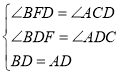
∴△BDF≌△ACD(AAS),
∴BF=AC;
(2)连接CF,
∵△BDF≌△ADC,
∴DF=DC,
∴△DFC是等腰直角三角形.
∵CD=3,CF=![]() CD=3
CD=3![]() ,
,
∵AB=BC,BE⊥AC,
∴AE=EC,BE是AC的垂直平分线.
∴AF=CF,
∴AF=3![]() .
.


科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() (其中
(其中![]() 为常数,且
为常数,且![]() ),则称点
),则称点![]() 为点
为点![]() 的“
的“![]() 之雅礼点”.例如:
之雅礼点”.例如:![]() 的“
的“![]() 之雅礼点”为
之雅礼点”为![]() ,即
,即![]() .
.
(1)①点![]() 的 “
的 “![]() 之雅礼点”
之雅礼点” ![]() 的坐标为___________;
的坐标为___________;
②若点![]() 的“
的“![]() 之雅礼点”
之雅礼点” ![]() 的坐标为
的坐标为![]() ,请写出一个符合条件的点
,请写出一个符合条件的点![]() 的坐标_________;
的坐标_________;
(2)若点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的“
的“![]() 之雅礼点”为
之雅礼点”为![]() 点,且
点,且![]() 为等腰直角三角形,则
为等腰直角三角形,则![]() 的值为____________;
的值为____________;
(3)在(2)的条件下,若关于![]() 的分式方程
的分式方程![]() 无解,求
无解,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数![]() 与
与![]() 满足
满足![]() ,
,![]() ,
,![]() ,则称这两个函数互为“旋转函数”.
,则称这两个函数互为“旋转函数”.
求函数![]() 的“旋转函数”.
的“旋转函数”.
小明是这样思考的:由函数![]() 可知,
可知,![]() ,
,![]() ,
,![]() ,根据
,根据![]() ,
,![]() ,
,![]() ,求出
,求出![]() ,
,![]() ,
,![]() ,就能确定这个函数的“旋转函数”.
,就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面问题:
(1)直接写出函数![]() 的“旋转函数”;
的“旋转函数”;
(2)若函数![]() 与
与![]() 互为“旋转函数”,求
互为“旋转函数”,求![]() 的值;
的值;
(3)已知函数![]() 的图象与
的图象与![]() 轴交于点A、B两点(A在B的左边),与
轴交于点A、B两点(A在B的左边),与![]() 轴交于点C,点A、B、C关于原点的对称点分别是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数
轴交于点C,点A、B、C关于原点的对称点分别是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数![]() 互为“旋转函数”。
互为“旋转函数”。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座抛物线型拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m, 就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.
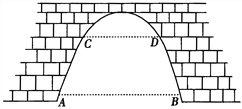
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=![]() ,求CG的长度;
,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农八师石河子市某中学初三(1)班的学生,在一次数学活动课中,来到市游憩广场,测量坐落在广场中心的王震将军的铜像高度,已知铜像底座的高为3.5m.某小组的实习报告如下.请你计算出铜像的高(结果精确到0.1m)
实习报告2003年9月25日
题目1 | 测量底部可以到达的铜像高 | |||
| ||||
测 得 数 据 | 测量项目 | 第一次 | 第二次 | 平均值 |
BD的长 | 12.3m | 11.7m | ||
测倾器CD的高 | 1.32m | 1.28m | ||
倾斜角 | α=30°56' | α=31°4' | ||
计 算 | ||||
结果 | ||||
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() 于点
于点![]() .
.
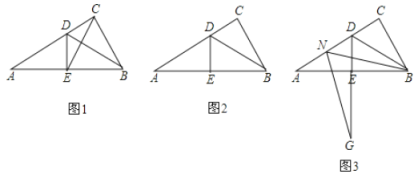
(1)如图![]() ,连接
,连接![]() ,求证:
,求证:![]() 是等边三角形;
是等边三角形;
(2)点![]() 是线段
是线段![]() 上的一点(不与点
上的一点(不与点![]() 重合),以
重合),以![]() 为一边,在
为一边,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延长线于点
延长线于点![]() ,请你在图
,请你在图![]() 中画出完整图形,并直接写出
中画出完整图形,并直接写出![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(3)如图![]() ,点
,点![]() 是线段
是线段![]() 上的一点,以
上的一点,以![]() 为一边,在
为一边,在![]() 的下方作
的下方作![]() ,
,![]() 交
交![]() 延长线于点
延长线于点![]() ,试探究
,试探究![]() 与
与![]() 数量之间的关系,并说明理由.
数量之间的关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com