
【题目】为了了解某校九年级全体男生![]() 米跑步的成绩,随机抽取了部分男生进行测试.并将测试成绩分为
米跑步的成绩,随机抽取了部分男生进行测试.并将测试成绩分为![]() 四个成绩,绘制了如下不完整的统计图表.
四个成绩,绘制了如下不完整的统计图表.
成绩等级频数分布表
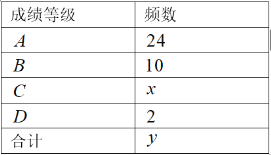
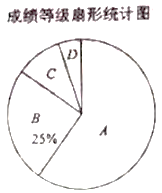
根据图表信息解答下列问题:
![]() 填空:
填空:![]() _____,
_____,![]() _____,扇形统计图中表示
_____,扇形统计图中表示![]() 的扇形的圆心角度数为____度;
的扇形的圆心角度数为____度;
![]() 甲、乙、丙是
甲、乙、丙是![]() 等级中的
等级中的![]() 名学生.学习决定从这
名学生.学习决定从这![]() 名学生中随机抽取
名学生中随机抽取![]() 名来介绍体育锻炼经验,用列表法或画树状图法,求同时抽到甲、乙
名来介绍体育锻炼经验,用列表法或画树状图法,求同时抽到甲、乙![]() 学生的概率.
学生的概率.
【答案】(1)4,40,216;(2)![]() .
.
【解析】
(1)先根据B等级的扇形统计图和频数分布表可求出抽取的总人数y,由此即可得求出x的值,再求出A等级的人数占比,然后乘以![]() 即可得所求圆心角的度数;
即可得所求圆心角的度数;
(2)先画出树状图,再找出从甲、乙、丙中随机抽取![]() 名的所有可能的结果,然后找出同时抽到甲、乙
名的所有可能的结果,然后找出同时抽到甲、乙![]() 学生的结果,最后利用概率公式计算即可得.
学生的结果,最后利用概率公式计算即可得.
(1)由B等级的扇形统计图和频数分布表得:![]()
则![]()
A等级的人数占比为![]()
则所求的圆心角的度数为![]()
故答案为:4,40,216;
(2)依题意,画树状图如下所示:
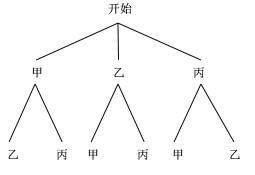
由图可知,从甲、乙、丙中随机抽取![]() 名的所有可能的结果有6种,它们每一种出现的可能性都相等,其中,同时抽到甲、乙
名的所有可能的结果有6种,它们每一种出现的可能性都相等,其中,同时抽到甲、乙![]() 学生的结果有2种
学生的结果有2种
则所求的概率为![]()
答:同时抽到甲、乙![]() 学生的概率
学生的概率![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,甲、乙只捕捞船同时从A港出海捕鱼,甲船以每小时15![]() km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
(1)甲船从C处出发追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为边
为边![]() 上的中线,点
上的中线,点![]() 为
为![]() 延长线上一点,连接
延长线上一点,连接![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]() .
.
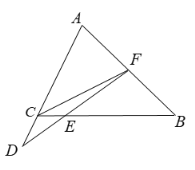
(1)求证:![]() ;
;
(2)在图中找出与![]() 相等的线段,并证明;
相等的线段,并证明;
(3)若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知OA是⊙O的半径,OA=1,点P是OA上一动点,过P作弦BC⊥OA,连接AB、AC.

(1)如图1,若P为OA中点,则AC=______,∠ACB=_______°;
(2)如图2,若移动点P,使AB、CO的延长线交于点D.记△AOC的面积为S1,△BOD的面积为S2.△AOD的面积为S3,且满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k<0)与反比例函数![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)

(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄金三角形就是一个等腰三角形,且其底与腰的长度比为黄金比值![]() .如图1,在黄金
.如图1,在黄金![]() 中,
中,![]() ,点
,点![]() 是
是![]() 上的一动点,过点
上的一动点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
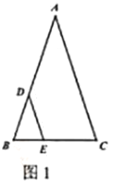
![]() 当点
当点![]() 是线段
是线段![]() 的中点时,
的中点时,![]() ;当点
;当点![]() 是线段
是线段![]() 的三等分点时,
的三等分点时,![]() ;
;
![]() 把
把![]() 绕点
绕点![]() 逆时针旋转到如图2所示位置,连接
逆时针旋转到如图2所示位置,连接![]() ,判断
,判断![]() 的值是否变化,并给出证明;
的值是否变化,并给出证明;
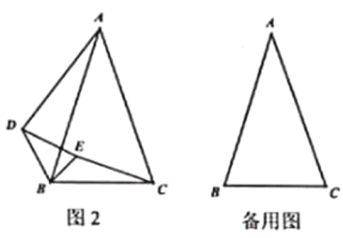
![]() 把
把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() 请直接写出线段
请直接写出线段![]() 的长的取值范围.
的长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条直线把矩形分割成两个矩形,其中一个为黄金矩形 (宽与长的比为![]() 的矩形),则称这条直线为该矩形的黄金线.例如图所示的矩形
的矩形),则称这条直线为该矩形的黄金线.例如图所示的矩形![]() 中,直线
中,直线![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,显然直线
,显然直线![]() 是矩形
是矩形![]() 的黄金线.
的黄金线.
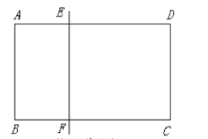
(1)如图,在矩形![]() 中,
中,![]() ,
,![]() .请在图中画出矩形
.请在图中画出矩形![]() 的其中一条黄金线
的其中一条黄金线![]() ,其中
,其中![]() 在
在![]() 边上,
边上,![]() 在
在![]() 边上,并标注出线段
边上,并标注出线段![]() 的长度;
的长度;
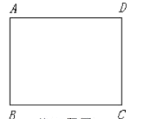
(2)将正方形纸片按图所示的方式折叠.
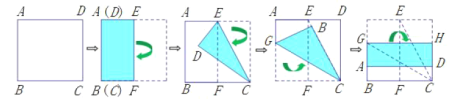
如图所示,按上述方法折叠所得到的折痕![]() 是否为正方形
是否为正方形![]() 的黄金线?请说明理由.
的黄金线?请说明理由.
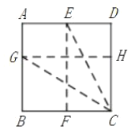
(3)在矩形![]() 中,
中,![]() ,
,![]() ,己知矩形
,己知矩形![]() 的黄金线
的黄金线![]() 恰好将矩形
恰好将矩形![]() 分割成两个黄金矩形,则
分割成两个黄金矩形,则![]() ______(只要求直接写出其中三个答案).
______(只要求直接写出其中三个答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE,连接DE并延长交射线AP于点F,连接BF
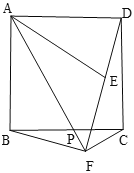
(1)若![]() ,直接写出
,直接写出![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)求证:![]() .
.
(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD, ∠F=90°,则∠1、∠2、∠3间的关系正确的是( )
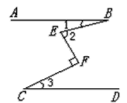
A.∠2=∠1+∠3B.∠1+∠2+∠3=90°
C.∠2+∠3-∠1=90°D.∠1+∠3-∠2=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com