
 已知2y-3与-3x-1成正比例,且x=2时,y=5.
已知2y-3与-3x-1成正比例,且x=2时,y=5.分析 (1)由2y-3与-3x-1成正比例,设2y-3=k(-3x-1),将x=2,y=5代入求出k的值,代入即可确定出y与x的函数关系式.
(2)先分别计算出函数值为-1和1所对应的自变量的值,然后根据一次函数的性质求解.
(3)根据平移的性质即可求得.
解答 解:(1)由2y-3与-3x-1成正比例,设2y-3=k(-3x-1),
将x=2,y=5代入得:10-3=k(-6-1),
解得:k=-1,
则y与x的关系式为y=$\frac{3}{2}$x+2;
画图如下: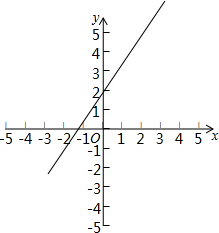
(2)当y=-1时,$\frac{3}{2}$x+2=-1,解得x=-2;当y=2时$\frac{3}{2}$x+2=2,解得x=0,
所以当-1≤y≤2时,x的取值范围为-2≤x≤0.
(3)根据平移的性质得出y=$\frac{3}{2}$x-1;
故答案为
如图: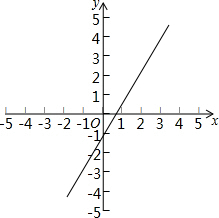
点评 此题考查了待定系数法求一次函数解析式,一次函数的图象以及一次函数图象的几何变换,熟练掌握待定系数法是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时30海里的速度航行半小时到达C处,同时捕鱼船低速航行到A点的正北1.5海里D处,渔政船航行到点C处时测得点D在南偏东53°方向上.
如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时30海里的速度航行半小时到达C处,同时捕鱼船低速航行到A点的正北1.5海里D处,渔政船航行到点C处时测得点D在南偏东53°方向上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
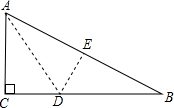 如图,一中江县进行纸片,AC=6cm,AB=10cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图,一中江县进行纸片,AC=6cm,AB=10cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )| A. | 3cm | B. | 5cm | C. | 3$\sqrt{5}$cm | D. | 9$\sqrt{5}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
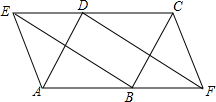 如图,以平行四边形ABCD的边分别向外作等边三角形ADE和BCF
如图,以平行四边形ABCD的边分别向外作等边三角形ADE和BCF查看答案和解析>>
科目:初中数学 来源: 题型:填空题
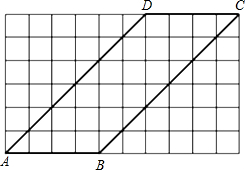 如图,在正方形网格中有一个边长为4的平行四边形ABCD
如图,在正方形网格中有一个边长为4的平行四边形ABCD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com