
【题目】已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧
(1)若AB=18,DE=8,线段DE在线段AB上移动
①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;
(2)若AB=2DE,线段DE在直线AB上移动,且满足关系式![]() ,则
,则![]() ______.
______.
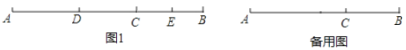
【答案】(1)①7;②3或5;(2)![]() .
.
【解析】
(1)①根据AB的长和![]() 可求出AC和BC,根据中点的定义可得CE,再由
可求出AC和BC,根据中点的定义可得CE,再由![]() 可得CD,最后根据
可得CD,最后根据![]() 计算即可得;
计算即可得;
②设![]() ,因点F(异于A、B、C点)在线段AB上,
,因点F(异于A、B、C点)在线段AB上,![]() 可知
可知![]() ,
,![]() 和
和![]() ,所以需分2种情况进行讨论:
,所以需分2种情况进行讨论:![]() 和
和![]() ,如图2、3(见解析),先根据已知条件判断点E、F位置,再将EF和CE用含x的式子表示出来,最后代入
,如图2、3(见解析),先根据已知条件判断点E、F位置,再将EF和CE用含x的式子表示出来,最后代入![]() 求解即可;
求解即可;
(2)设![]() ,先判断出DE在AB上的位置,再根据
,先判断出DE在AB上的位置,再根据![]() 得出x和y满足的等式,然后将其代入
得出x和y满足的等式,然后将其代入![]() 化简即可得.
化简即可得.
(1)①![]()
![]()
又![]() E为BC中点
E为BC中点
![]()
![]()
![]()
![]() ;
;
②设![]() ,因点F(异于A、B、C点)在线段AB上,
,因点F(异于A、B、C点)在线段AB上,![]() 可知:
可知:
![]() ,
,![]() 和
和![]()
当![]() 时,
时,![]()
![]()
![]()
![]()
此时可画图如图2所示,代入![]() 得:
得:![]()
解得:![]() ,即AD的长为3
,即AD的长为3
当![]() 时,
时,![]()
![]()
![]()
![]()
此时可画图如图3所示,代入![]() 得:
得:![]()
解得:![]() ,即AD的长为5
,即AD的长为5
综上,所求的AD的长为3或5;
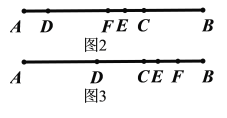
(2)①若DE在如图4的位置
设![]() ,则
,则![]()
![]()
又![]()
![]()
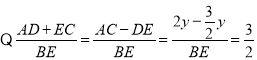
![]() (不符题设,舍去)
(不符题设,舍去)
②如DE在如图5的位置
设![]() ,则
,则![]()
![]()
又![]()
![]()
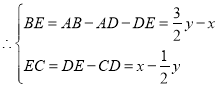
代入![]() 得:
得: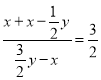
解得:![]()
则![]() .
.
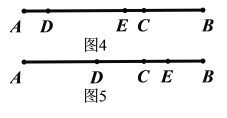


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两支“徒步队”到野外沿相同路线徒步,徒步的路程为24千米.甲队步行速度为4千米/时,乙队步行速度为6千米/时.甲队出发1小时后,乙队才出发,同时乙队派一名联络员跑步在两队之间来回进行一次联络(不停顿),他跑步的速度为10千米/时.
(1)乙队追上甲队需要多长时间?
(2)联络员从出发到与甲队联系上后返回乙队时,他跑步的总路程是多少?
(3)从甲队出发开始到乙队完成徒步路程时止,何时两队间间隔的路程为1千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列每一列数,按规律填空
(1)![]() , ,……
, ,……
(2)![]() , ,……
, ,……
(3)![]() , ,……
, ,……
(4)在(1)列数中第100个数是 ,在(2)列数中第200个数是 ,在(3)列数中第199个数是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
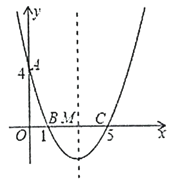
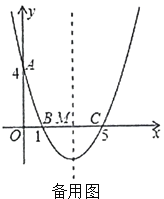
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 两点,其对称轴与
两点,其对称轴与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)连接![]() ,在直线
,在直线![]() 的下方的抛物线上,是否存在一点
的下方的抛物线上,是否存在一点![]() ,使
,使![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⑴ 阅读理解:我们知道在直角三角形中,有无数组勾股数,例如:5、12、13;9、40、41;……但其中也有一些特殊的勾股数,例如:3、4、5;是三个连续正整数组成的勾股数.
解决问题:① 在无数组勾股数中,是否存在三个连续偶数能组成勾股数?
答: ,若存在,试写出一组勾股数: .
② 在无数组勾股数中,是否还存在其它的三个连续正整数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
③ 在无数组勾股数中,是否存在三个连续奇数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
⑵ 探索升华:是否存在锐角△ABC三边也为连续正整数;且同时还满足:∠B>∠C>∠A;∠ABC=2∠BAC?若存在,求出△ABC三边的长;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
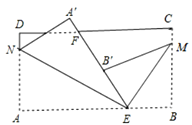
【题目】如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF,将∠BEF对折 B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′得折痕EN,若∠BEM=62°15′ ,则∠AEN=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
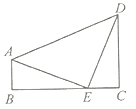
【题目】1876年,美国总统Garfield用如图所示的两个全等的直角三角形证明了勾股定理,若图中![]() ,
,![]() ,
,![]() ,则下面结论错误的是( )
,则下面结论错误的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 是等腰直角三角形
是等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
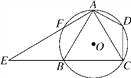
【题目】如图,已知四边形ABCD内接于⊙O,A是![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F,E,且![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)为培养学生数学学习兴趣,某校七年级准备开设“神奇魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课(每位学生必须且只选其中一门).
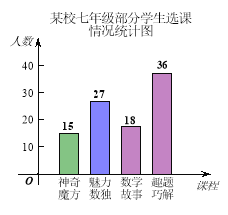
(1)学校对七年级部分学生进行选课调查,得到如图所示的统计图,根据该统计图,请估计该校七年级480名学生选“数学故事”的人数。
(2)学校将选“数学故事”的学生分成人数相等的A,B,C三个班,小聪、小慧都选择了“数学故事”,已知小聪不在A班,求他和小慧被分到同一个班的概率.(要求列表或画树状图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com