
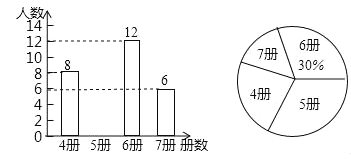
【题目】高尔基说:“书,是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况,某校随机抽查了部分学生阅读课外书册数的情况,并绘制出如下统计图,其中条形统计图因为破损丢失了阅读5册书数的数据.
(1)求条形图中丢失的数据,并写出阅读书册数的众数和中位数;
(2)根据随机抽查的这个结果,请估计该校1200名学生中课外阅读5册书的学生人数;
(3)若学校又补查了部分同学的课外阅读情况,得知这部分同学中课外阅读最少的是6册,将补查的情况与之前的数据合并后发现中位数并没有改变,试求最多补查了多少人?
科目:初中数学 来源: 题型:
【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB的最小覆盖圆就是以线段AB为直径的圆.
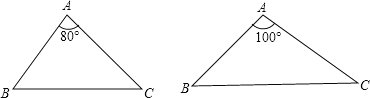
(1)请分别作出下图中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为2,O到顶点A的距离为5,点B在⊙O上,点P是线段AB的中点,若B在⊙O上运动一周.
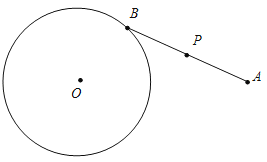
(1)点P的运动路径是一个圆;
(2)△ABC始终是一个等边三角形,直接写出PC长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上的一个动点(点
上的一个动点(点![]() 与点
与点![]() 不重合),点
不重合),点![]() 是线段
是线段![]() 上的一个动点(点
上的一个动点(点![]() 与点
与点![]() 不重合),连接
不重合),连接![]() ,过点
,过点![]() 作
作![]() 的垂线,交射线
的垂线,交射线![]() 于点
于点![]() 连接
连接![]() .设
.设![]()
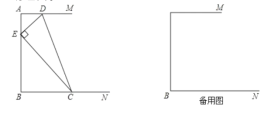
(1)当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式,并写出它的定义域;
的函数关系式,并写出它的定义域;
(2)在(1)的条件下,取线段![]() 的中点
的中点![]() ,连接
,连接![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)如果动点![]() 在运动时,始终满足条件
在运动时,始终满足条件![]() 那么请探究:
那么请探究:![]() 的周长是否随着动点
的周长是否随着动点![]() 的运动而发生变化?请说明理由。
的运动而发生变化?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在![]() 中,
中,![]() ,
,![]() 是平面内任意一点,将线段
是平面内任意一点,将线段![]() 绕点
绕点![]() 顺时针旋转与
顺时针旋转与![]() 相等的角度,得到线段
相等的角度,得到线段![]() ,连接
,连接![]() .
.
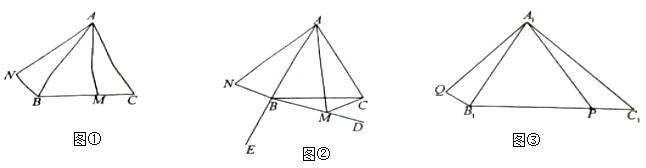
①如图①,若![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() ,
,![]() ,则
,则![]() 的大小
的大小![]() (度),
(度),![]() 的长
的长![]() ;
;
②如图②,点![]() 是
是![]() 延长线上的一点,若
延长线上的一点,若![]() 是
是![]() 内部射线
内部射线![]() 上任意一点,连接
上任意一点,连接![]() ,
,![]() 与
与![]() 的数量关系是什么?
的数量关系是什么?![]() 与
与![]() 的数量关系是什么?并分别给予证明:
的数量关系是什么?并分别给予证明:
(2)如图③,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的任意一点,连接
上的任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() ,求线段
,求线段![]() 长度的最小值(直接写出结果即可).
长度的最小值(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
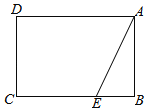
【题目】已知矩形ABCD中,AB=2,BC=m,点E是边BC上一点,BE=1,连接AE.
(1)沿AE翻折△ABE使点B落在点F处,
①连接CF,若CF∥AE,求m的值;
②连接DF,若![]() ≤DF≤
≤DF≤![]() ,求m的取值范围.
,求m的取值范围.
(2)△ABE绕点A顺时针旋转得△AB1E1,点E1落在边AD上时旋转停止.若点B1落在矩形对角线AC上,且点B1到AD的距离小于![]() 时,求m的取值范围.
时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求二次函数![]() 的图象如图所示,其对称轴为直线
的图象如图所示,其对称轴为直线![]() ,与
,与![]() 轴的交点为
轴的交点为![]() 、
、![]() ,其中
,其中![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中,正确的结论有( )
;其中,正确的结论有( )
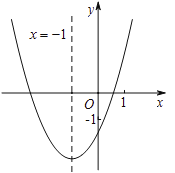
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
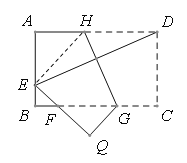
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上E处,EQ与BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,则△EBF的周长是______________ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中,三个顶点的坐标分别为A(0,4),B(2,2),C(4,6)(正方形网格中,每个小正方形的边长均为1).
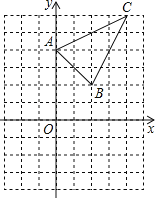
(1)画出△ABC向下平移5个单位长度得到的△A1B1C1,并写出点B1的坐标;
(2)以点O为位似中心,在第三象限内画出△A2B2C2,使△A2B2C2与△ABC位似,且相似比为1:2,直接写出点C2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com