Question

【题目】如图，⊙是的外接圆，，，交的延长线于点，交于点.

(1)求证:是⊙的切线;

(2)若，.求⊙的半径和线段的长.

Answer 1

【答案】(1)证明见解析；(2)⊙的半径为4和线段的长为.

【解析】

（1）连结OA，根据圆周角定理求得∠AOC=90°，又因AD∥OC，根据平行线的性质可得∠AOD=90°，即OA⊥OC，即可证得 AD是⊙O的切线；（2）设⊙O的半径为R，则OA=R，OE=R-2，AE=2，在Rt△OAE中，根据勾股定理列出方程，解方程求得R的长，即可求得⊙O的半径；延长CO交⊙O于F，连接AF，可得△CEB∽△AEF，根据相似三角形的性质可得 ，代入数据求得BE的值即可．

（1）证明：连结OA，如图，

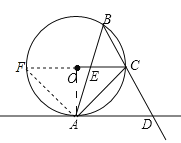
∵∠ABC=45°，

∴∠AOC=2∠ABC=2×45°=90°，

∴AD∥OC，

∴∠AOD=90°，即OA⊥OC，

∴AD是⊙O的切线；

（2）设⊙O的半径为R，则OA=R，OE=R-2，AE=2，

在Rt△OAE中，∵AO2+OE2=AE2，

∴R2+（R-2）2=（2）2，

解得R=4或R=-2（舍去），

即⊙O的半径为4；

延长CO交⊙O于F，连接AF，

则△CEB∽△AEF，

∴ ，

∵EF=2R-2=6，

∴

∴BE=．