
【题目】在平面直角坐标系中点![]() 、
、![]() 分别是
分别是![]() 轴、
轴、![]() 轴上的点且
轴上的点且![]() 点的坐标是
点的坐标是![]() ,
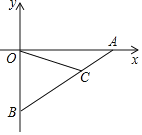
,![]() .点
.点![]() 在线段
在线段![]() 上,是靠近点
上,是靠近点![]() 的三等分点.点
的三等分点.点![]() 是
是![]() 轴上的点,当
轴上的点,当![]() 是等腰三角形时,点
是等腰三角形时,点![]() 的坐标是__________.
的坐标是__________.
【答案】(0,![]() )或(0,-
)或(0,-![]() )或(0,-
)或(0,-![]() )或(0,-2)
)或(0,-2)
【解析】
根据条件可得AC=2,过点C作CD⊥OA,由勾股定理得到OC=![]() ,再分以下三种情况求解:①当OP=OC时,可直接得出点P的坐标为(0,
,再分以下三种情况求解:①当OP=OC时,可直接得出点P的坐标为(0,![]() )或(0,-
)或(0,-![]() );②当PO=PC时,点P在OC的垂直平分线PE上,先求出直线OC的解析式,从而可求出直线PE的解析式,最后可求得P(0,-
);②当PO=PC时,点P在OC的垂直平分线PE上,先求出直线OC的解析式,从而可求出直线PE的解析式,最后可求得P(0,-![]() );③当CO=CP时,根据OP=2|yC|=2×1=2,求得P(0,-2).
);③当CO=CP时,根据OP=2|yC|=2×1=2,求得P(0,-2).
解:∵点B坐标是(0,-3),∠OAB=30°,
∴AB=2×3=6,AO=3![]() ,
,
∵点C在线段AB上,是靠近点A的三等分点,
∴AC=2,
过点C作CD⊥OA于D,
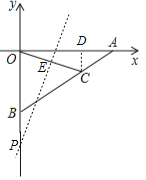
∴CD=![]() AC=1,
AC=1,
∴AD=![]() CD=
CD=![]() ,
,
∴OD=OA-AD=3![]() -
-![]() =2
=2![]() ,
,
∴OC=![]() .
.
∵△OCP为等腰三角形,分以下三种情况:
①当OP=OC=![]() 时,点P的坐标为(0,
时,点P的坐标为(0,![]() )或(0,-
)或(0,-![]() );
);
②当PO=PC时,点P在OC的垂直平分线PE上,其中E为OC的中点,
∴点E的坐标为(![]() ,-
,-![]() ),
),
设直线OC的解析式为y=k1x,将点C(2![]() ,-1)代入得k1=-
,-1)代入得k1=-![]() ,
,
则可设直线PE的解析式为y=k2x+b,则k1·k2=-1,∴k2=2![]() ,
,
∴将点E(![]() ,-
,-![]() )代入y=2
)代入y=2![]() x+b,得b=-
x+b,得b=-![]() ,
,
∴P(0,![]() ),
),
③当CO=CP时,OP=2|yC|=2×1=2,
∴P(0,-2),
综上所述,当△OCP为等腰三角形时,点P的坐标为(0,![]() )或(0,-
)或(0,-![]() )或(0,-
)或(0,-![]() )或(0,-2),
)或(0,-2),
故答案为:(0,![]() )或(0,-
)或(0,-![]() )或(0,-
)或(0,-![]() )或(0,-2).
)或(0,-2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知∠MAN=120°,AC平分∠MAN.
(1)在图1中,若∠ABC=∠ADC=90°,求证:AB+AD=AC;
(2)在图2中,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
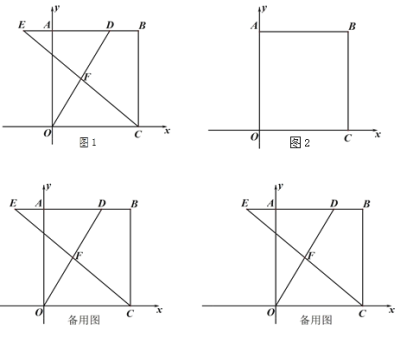
【题目】矩形OABC的顶点O与坐标原点重合,点B的坐标为(6,8),动点D、E分别从点B、A同时出发,沿射线BA运动,点D、E的运动速度均为每秒2个单位,设D、E的运动时间为t秒.连接OD、CE交于点F.
(1)如图1,求点F的纵坐标;
(2)若点G为OA的中点,在点D、E运动过程中,设△GEF的面积为y,求y与t的关系式;
(3)在(2)的条件下,连接BG,线段BG、OD交于点K,若![]() ,坐标平面内是否存在点M,使以D、E、K、M为顶点的四边形为平行四边形,如果存在,请求出点M的坐标;如果不存在,请说明理由.
,坐标平面内是否存在点M,使以D、E、K、M为顶点的四边形为平行四边形,如果存在,请求出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB交x轴于点A(![]() ,0),交y轴于点B(0,
,0),交y轴于点B(0,![]() ),且
),且![]() .b满足
.b满足![]()
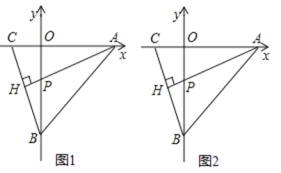
(1)求证:OA=OB;
(2)如图1,若C的坐标为(-1,0),且AH⊥BC于点H,AH交OB于点P,试求点P的坐标;
(3)如图2,连接OH,求证:∠OHP=45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象经过A、B两点,与x轴交于点C,则此一次函数的解析式为__________,△AOC的面积为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
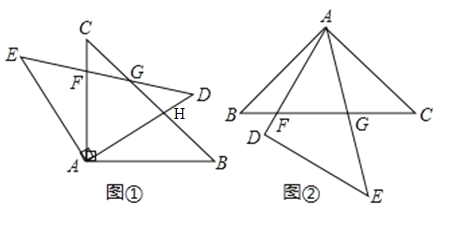
【题目】(1)如图①所示,将![]() 绕顶点
绕顶点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 角,得到
角,得到![]() ,
,![]() ,
,![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .求证:
.求证:![]() ;
;
(2)如图②所示,![]() 和
和![]() 是全等的等腰直角三角形,
是全等的等腰直角三角形,![]() ,
,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,请说明
,请说明![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com