
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
| (1+3)×3 |
| 2 |
| (1+4)×4 |
| 2 |
| (1+5)×5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2012届江苏金坛市七年级期中测试数学卷(带解析) 题型:解答题
观察下列等式,并回答有关问题: ;
; ;
; ;
;
【小题1】若n为正整数,猜想 ;
;
【小题2】利用上题的结论比较 与
与 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏金坛市七年级期中测试数学卷(解析版) 题型:解答题
观察下列等式,并回答有关问题:
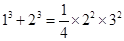 ;
;
 ;
;
 ;
;
1.若n为正整数,猜想 ;
;
2.利用上题的结论比较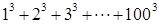 与
与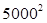 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com