解:(1)设函数解析式为y=-

(x+

)
2+c,
将B(0,-4)代入解析式得,-4=-

(0+

)
2+c,
解得,c=

,
函数解析式为y=-

(x+

)
2+

;
(2)依题意知OE平行且等于AC,
∴四边形OEAC为平行四边形,
又∵OA为平行四边形OEAC的对角线,
∴S
?OECA=2•S
△AEO=24,即S
△AEO=12,
∴

•OA•|y
E|=12,
又∵A(-6,0),OA=6,
y
E=-

(x+

)
2+

,
∴

×6×[-

(x+

)
2+

]=12,
解得,x
1=-3,x
2=-4,
∴E
1(-3,4)或E
2(-4,4),
∴这样的点有两个.
当E
1(-3,4)时,有AE=OE,此时平行四边形为菱形
当E
2(-4,4)时,AE≠OE,AE不垂直于OE,此时四边形OEAC为平行四边形;
(3)|x
E|+|x
C|的值不变,|x
E|+|x
C|=6,
证明:过E作EM⊥AO于M,过C作CN⊥AO于N,
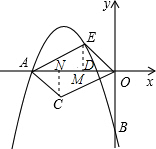
则|x
E|=OM,|x
C|=ON,
∵四边形OEAC是平行四边形,
∴OE∥AC,OE=AC,
∴△EMO≌△CNA,
∴OM=AN,
∴OM+ON=AN+ON=OA=6,即|x
E|+|x
C|=6.
分析:(1)设出函数顶点式,将B(0,-4)代入解析式即可;
(2)假设存在这样的点,根据S=24得到S
?OECA=2•S
△AEO=24,即S
△AEO=12,然后将坐标代入求解即可.
(3)过E作 EM⊥AO于M,过C作CN⊥AO于N,将OM+ON转化为AN+ON=OA=6即可解答.
点评:本题考查了二次函数综合题,对于存在性问题,先假设其存在,然后求解,若能的出结果,则存在,否则不存在.

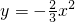 相同,且对称轴为
相同,且对称轴为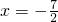 ,交x轴于A、D两点(A在D左边),交y轴于B(0,-4).
,交x轴于A、D两点(A在D左边),交y轴于B(0,-4).
 (x+
(x+ )2+c,
)2+c, (0+
(0+ )2+c,
)2+c, ,
, (x+
(x+ )2+
)2+ ;
; •OA•|yE|=12,
•OA•|yE|=12, (x+
(x+ )2+
)2+ ,
, ×6×[-
×6×[- (x+
(x+ )2+
)2+ ]=12,
]=12,


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案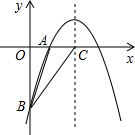 如图,已知二次函数y=ax2+bx+c的图象的形状与抛物线y=-
如图,已知二次函数y=ax2+bx+c的图象的形状与抛物线y=-