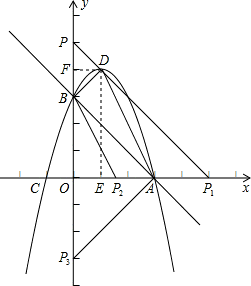
抛物线y=-x2+bx+c经过直线y=-x+3与坐标轴的两个交点A、B,抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)试判断△ABD的形状,并证明你的结论;
(3)在坐标轴上是否存在点P,使得以点P、A、B、D为顶点的四边形是梯形?若存在,求出点P的坐标;若不存在,说明理由.
解:(1)如图,∵直线y=-x+3与坐标轴的两个交点为A、B,
∴点A的坐标为(3,0),点B的坐标为(0,3).
又∵抛物线经过点A、B,
∴
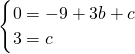
,
解得
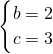
∴抛物线的解析式为y=x
2+2x+3.
(2)△ABD为直角三角形.
∵抛物线y=-x
2+2x+3的顶点D的坐标为(1,4),过点D作DE⊥x轴于E,DE⊥y轴于F.
∴可求BD=

,AB=3

,AD=2

.
∴AB
2+BD
2=AD
2.
∴△ABD为直角三角形.
(3)如图,坐标轴上存在点P,使得以点P、A、B、D为顶点的四边形是梯形.
分为三种情况:
①以AB为底边.
过点D作PD∥AB交y轴于点P.
∵可知∠ABO=45°,
∴∠DPO=45°.
∴可求PF=1.
∴PO=5.即点P(0,5).
若过点D作P
1D∥AB交x轴于点P
1 .
同理可求P
1坐标为(5,0).
②以AD为底.
过点B作P
2B∥AD交x轴于点P
2 .
利用△ADE∽△P
2BO可求出点P
2的坐标为(

,0).
③以BD为底.
过点A作P
3A∥BD交y轴于点P
3 .
∵∠ABD=90°,
∴∠BAP
3=90°.
又∵∠BAO=45°,
∴∠P
3AO=45°.
∴AO=P
3O=3.
∴点P
3的坐标为(0,-3).
综上所述,点P坐标分别为(5,0)或(

,0)或(0,5)或(0,-3).
分析:(1)由直线AB的解析式可求出点A、B的坐标;再由待定系数法求出抛物线的解析式.
(2)由(1)的抛物线解析式能求出顶点D的坐标,然后求出AB、AD、BD三边的长,据此判断△ABD的形状.
(3)应分三种情况:
①过点D作AB的平行线PD,那么点P为直线PD与x或y轴的交点;可先求出∠OPD的度数,根据这个特殊度数来求出OP的长,由此得出点P的坐标;
②过点B作AD的平行线BP,此时△OBP、△EDA(如图)相似,根据相似三角形得到的比例线段求出OP的长,据此求出点P的坐标;
③过点A作BD的平行线AP,解题思路同①.
点评:此题主要考查了利用待定系数法确定函数解析式、直角三角形的判定、梯形的判定等综合知识;最后一题的解题方法较多,还可以先求出另一底的直线解析式,再求出直线与坐标轴的交点即可.

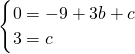 ,
,

 ,AB=3
,AB=3 ,AD=2
,AD=2 .
. ,0).
,0). ,0)或(0,5)或(0,-3).
,0)或(0,5)或(0,-3).

 阅读快车系列答案
阅读快车系列答案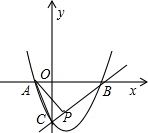 A是抛物线与x轴的另一个交点.
A是抛物线与x轴的另一个交点. 已知一元二次方程-x2+bx+c=0的两个实数根是m,4,其中0<m<4.
已知一元二次方程-x2+bx+c=0的两个实数根是m,4,其中0<m<4.