
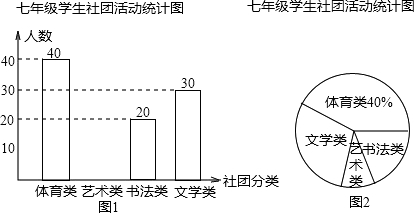
分析 (1)由体育类的人数除以所占的百分比即可求出调查的总学生数;由书法类的人数除以总人数求出百分比,乘以360即可得到结果;
(2)求出艺术类的人数,补全图1即可;
(3)用总人数乘文学类的百分比即可得到结果.
解答 解:(1)根据题意得:40÷40%=100(名);$\frac{20}{100}$×360°=72°,
故答案为:100;72;
(2)艺术的人数为100-(40+20+30)=10(名),补全统计图,如图所示: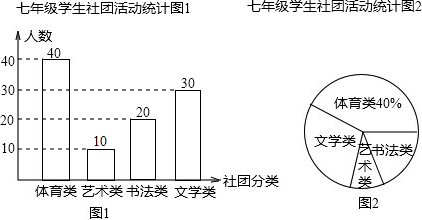
(3)1000×$\frac{30}{100}$=300(人),
该校七年级学生参加文学类社团的人数为300人.
点评 此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.


科目:初中数学 来源: 题型:填空题
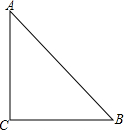 如图,已知在Rt△ABC中,∠C=90°,AC=BC=1,点D在边BC上,将△ABC沿直线AD翻折,使点C落在点C′处,联结AC′,直线AC′与边CB的延长线相交于点F.如果∠DAB=∠BAF,那么BF=$\sqrt{3}$-1.
如图,已知在Rt△ABC中,∠C=90°,AC=BC=1,点D在边BC上,将△ABC沿直线AD翻折,使点C落在点C′处,联结AC′,直线AC′与边CB的延长线相交于点F.如果∠DAB=∠BAF,那么BF=$\sqrt{3}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
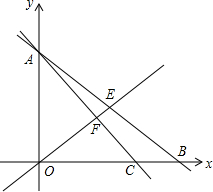 已知,如图,在y轴上有一点A(0,6),在x轴上有两点B(6,0)、C(5,0).
已知,如图,在y轴上有一点A(0,6),在x轴上有两点B(6,0)、C(5,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm,3cm,5cm | B. | 3cm,4cm,6cm | C. | 5cm,6cm,11cm | D. | 8cm,5cm,2cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对剡溪水质情况的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对某班50名同学体重情况的调查 | |
| D. | 对某品牌日光灯质量情况的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
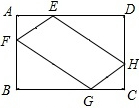 如图,在矩形ABCD中,AB=5,BC=6,点E,F,G,H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )
如图,在矩形ABCD中,AB=5,BC=6,点E,F,G,H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )| A. | $\left\{\begin{array}{l}{a+b=5}\\{a+2b=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=2b}\\{2a+b=6}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2a+b=5}\\{a+2b=6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2a+b=6}\\{a+2b=5}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5.4(1+x)2=6.3 | B. | 5.4(1-x)2=6.3 | C. | 6.3(1+x)2=5.4 | D. | 6.3(1-x)2=5.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com