
如图8-12,已知AE=CF,∠DAF=∠BCE,AD=CB.

图8-12
(1)问:△ADF与△CBE全等吗?请说明理由.
(2)如果将△BEC沿CA边方向平行移动,可有图8-13中3幅图,如上面的条件不变,结论仍成立吗?请选择一幅图说明理由.

图8-13
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
| 3 | 5 |
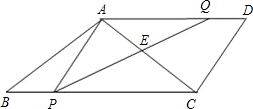 BC上移动(点P不与点B、C重合),点Q在射线AD上移动,且在移动的过程中始终有∠APQ=∠CAD,PQ交AC于点E.
BC上移动(点P不与点B、C重合),点Q在射线AD上移动,且在移动的过程中始终有∠APQ=∠CAD,PQ交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
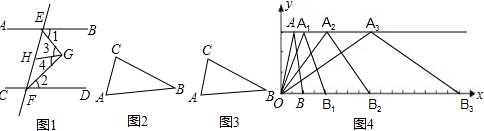
 我市关工委为了解本市九年级学生的睡眠时间情况,对我校若干名九年级学生的睡眠时间t(3~9小时之间)进行了抽查,将所得数据整理后,画出了频率分布直方图的一部分(如图).已知图中从左到右前五个小组的频率分别是0.04,0.12,0.20,0.28,0.24,第三小组的频数为20.请回答:
我市关工委为了解本市九年级学生的睡眠时间情况,对我校若干名九年级学生的睡眠时间t(3~9小时之间)进行了抽查,将所得数据整理后,画出了频率分布直方图的一部分(如图).已知图中从左到右前五个小组的频率分别是0.04,0.12,0.20,0.28,0.24,第三小组的频数为20.请回答:查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图8-12,已知AE=CF,∠DAF=∠BCE,AD=CB.
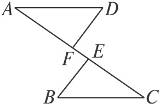
图8-12
(1)问:△ADF与△CBE全等吗?请说明理由.
(2)如果将△BEC沿CA边方向平行移动,可有图8-13中3幅图,如上面的条件不变,结论仍成立吗?请选择一幅图说明理由.
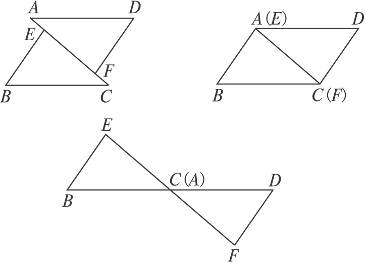
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com