
【题目】已知二次函数![]() (
(![]() ,
,![]() 为常数).
为常数).
(1)当![]() ,
,![]() 时,求二次函数的最小值;
时,求二次函数的最小值;
(2)当![]() 时,若在函数值
时,若在函数值![]() 的情况下,只有一个自变量
的情况下,只有一个自变量![]() 的值与其对应,求此时二次函数的解析式;
的值与其对应,求此时二次函数的解析式;
(3)当![]() 时,若在自变量
时,若在自变量![]() 的值满足
的值满足![]() ≤
≤![]() ≤
≤![]() 的情况下,与其对应的函数值
的情况下,与其对应的函数值![]() 的最小值为21,求此时二次函数的解析式.
的最小值为21,求此时二次函数的解析式.
【答案】(1)二次函数取得最小值-4;(2)![]() 或
或![]() ;
;
(3)![]() 或
或![]() .
.
【解析】
(1)当b=2,c=-3时,二次函数的解析式为![]() ,把这个解析式化为顶点式利用二次函数的性质即可求最小值.
,把这个解析式化为顶点式利用二次函数的性质即可求最小值.
(2)当c=5时,二次函数的解析式为![]() ,又因函数值y=1的情况下,只有一个自变量x的值与其对应,说明方程
,又因函数值y=1的情况下,只有一个自变量x的值与其对应,说明方程![]() 有两个相等的实数根,利用
有两个相等的实数根,利用![]() 即可解得b值,从而求得函数解析式.
即可解得b值,从而求得函数解析式.
(3)当c=b2时,二次函数的解析式为![]() ,它的图象是开口向上,对称轴为
,它的图象是开口向上,对称轴为![]() 的抛物线.分三种情况进行讨论,①对称轴位于b≤x≤b+3范围的左侧时,即
的抛物线.分三种情况进行讨论,①对称轴位于b≤x≤b+3范围的左侧时,即![]() <b;②对称轴位于b≤x≤b+3这个范围时,即b≤
<b;②对称轴位于b≤x≤b+3这个范围时,即b≤![]() ≤b+3;③对称轴位于b≤x≤b+3范围的右侧时,即
≤b+3;③对称轴位于b≤x≤b+3范围的右侧时,即![]() >b+3,根据列出的不等式求得b的取值范围,再根据x的取值范围b≤x≤b+3、函数的增减性及对应的函数值y的最小值为21可列方程求b的值(不合题意的舍去),求得b的值代入也就求得了函数的表达式.
>b+3,根据列出的不等式求得b的取值范围,再根据x的取值范围b≤x≤b+3、函数的增减性及对应的函数值y的最小值为21可列方程求b的值(不合题意的舍去),求得b的值代入也就求得了函数的表达式.
解:(1)当b=2,c=-3时,二次函数的解析式为![]() ,即
,即![]() .
.
∴当x=-1时,二次函数取得最小值-4.
(2)当c=5时,二次函数的解析式为![]() .
.
由题意得,方程![]() 有两个相等的实数根.
有两个相等的实数根.
有![]() ,解得
,解得![]() ,
,
∴此时二次函数的解析式为![]() 或
或![]() .
.
(3)当c=b2时,二次函数的解析式为![]() .
.
它的图象是开口向上,对称轴为![]() 的抛物线.
的抛物线.
①若![]() <b时,即b>0,
<b时,即b>0,
在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y随x的增大而增大,
故当x=b时,![]() 为最小值.
为最小值.
∴![]() ,解得
,解得![]() ,
,![]() (舍去).
(舍去).
②若b≤![]() ≤b+3,即-2≤b≤0,
≤b+3,即-2≤b≤0,
当x=![]() 时,
时,![]() 为最小值.
为最小值.
∴![]() ,解得
,解得![]() (舍去),
(舍去),![]() (舍去).
(舍去).
③若![]() >b+3,即b<-2,
>b+3,即b<-2,
在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y随x的增大而减小,
故当x=b+3时,![]() 为最小值.
为最小值.
∴![]() ,即
,即![]()
解得![]() (舍去),
(舍去),![]() .
.
综上所述,![]() 或b=-4.
或b=-4.
∴此时二次函数的解析式为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
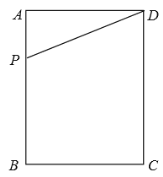
【题目】如图,在矩形ABCD中,AB=4,BC=3,点P是边AB上的一动点,连接DP,
(1)若将△DAP沿DP折叠,点A落在矩形的对角线上点A处,试求AP的长;
(2)点P运动到某一时刻,过点P作直线PE交BC于点E,将△DAP与△PBE分别沿DP与PE折叠,点A与点B分别落在点A,B处,若P,A,B三点恰好在同一直线上,且AB=2,试求此时AP的长.
(3)当点P运动到边AB的中点处时,过点P作直线PG交BC于点G,将△DAP与△PBG分别沿DP与PG折叠,点A与点B重合于点F处,请直接写出F到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
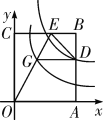
【题目】矩形OABC有两边在坐标轴的正半轴上,OA=4,OC=6,如图,双曲线y=![]() 与边AB交于点D,过点D作DG∥OA,交双曲线y=
与边AB交于点D,过点D作DG∥OA,交双曲线y=![]() (k>0)于点G,连接OG并延长交CB于点E,若∠EGD=∠EDG,则k的值为______.
(k>0)于点G,连接OG并延长交CB于点E,若∠EGD=∠EDG,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
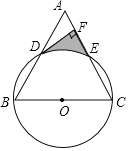
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校现有九年级学生800名,为了了解这些学生的体质健康情况,学校在开学初从中随机抽取部分学生进行体能测试(测试结果分成优秀、良好、合格、不合格四个等级),并将测试结果绘制成如图所示两幅不完整的统计图,请结合图中提供的信息解答下列问题:
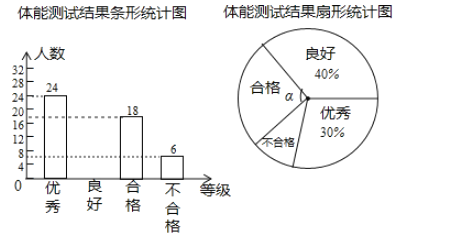
(1)本次抽取的学生人数共有____名,在扇形统计图中,“合格”等级所对应的圆心角![]() 的度数是______;
的度数是______;
(2)补全条形统计图;
(3)估计九年级学生中达到“合格”以上(含合格)等级的学生一共有多少名?
(4)若抽取的学生中,恰好有九年级(1)班的2名男生,2名女生,现要从这4人中随机抽取2人担任组长工作,请用列表法或树状图法求所抽取的2名学生中至少有1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
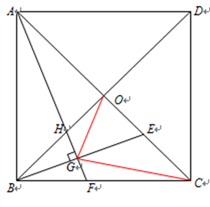
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BC于F,交B0于H,连接OG,CC.
(1)求证:AH=BE;
(2)试探究:∠AGO的度数是否为定值?请说明理由;
(3)若OG⊥CG,BG=![]() ,求△OGC的面积.
,求△OGC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com