
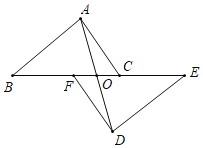
【题目】如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O.
(1)求证:△ABC≌△DEF;
(2)求证:AD与BE互相平分;
(3)若BF=5,FC=4,直接写出EO的长.
【答案】(1)详见解析;(2)详见解析;(3)7.
【解析】
(1)如图,连接BD,AE,根据已知条件得到BC=EF,根据平行线的性质得到∠ABC=∠DEF,∠ACB=∠DFE,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到AB=DE,根据平行四边形的判定和性质定理即可得到结论;
(3)根据线段的和差得到BE=BF+FC+CE=14,根据线段中点的定义即可得到结论.
(1)证明:如图,连接BD,AE,
∵FB=CE,
∴BC=EF,
又∵AB∥ED,AC∥FD,
∴∠ABC=∠DEF,∠ACB=∠DFE,
在△ABC和△DEF中, ,
,
∴△ABC≌△DEF(ASA);
(2)∵△ABC≌△DEF,
∴AB=DE,
又∵AB∥DE,
∴四边形ABDE是平行四边形,
∴AD与BE互相平分;
(3)解:∵FB=CE=5,FC=4,
∴BE=BF+FC+CE=14,
∵BO=OE=![]() BE=7.
BE=7.



科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到BC的距离.参考数据:sin73.7°≈![]() ,cos73.7°≈
,cos73.7°≈![]() ,tan73.7°≈
,tan73.7°≈![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个单位为 1 的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在 x 轴上、斜边长分别为 2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2019的横坐标为( )
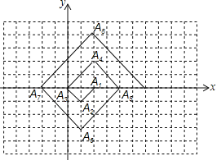
A.-1008B.2C.1D.1011
查看答案和解析>>
科目:初中数学 来源: 题型:
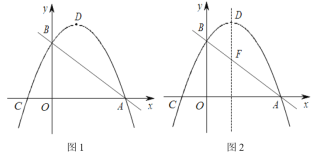
【题目】如图1,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点B;抛物线
与x轴交于点A,与y轴交于点B;抛物线![]() (a≠0)过A,B两点,与x轴交于另一点C(-1,0),抛物线的顶点为D.
(a≠0)过A,B两点,与x轴交于另一点C(-1,0),抛物线的顶点为D.
(1)求抛物线的解析式;
(2)在直线AB上方的抛物线上有一动点E,求出点E到直线AB的距离的最大值;
(3)如图2,直线AB与抛物线的对称轴相交于点F,点P在坐标轴上,且点P到直线 BD,DF的距离相等,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD=( )
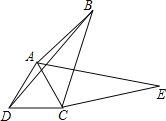
A.5B.5.5C.6D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
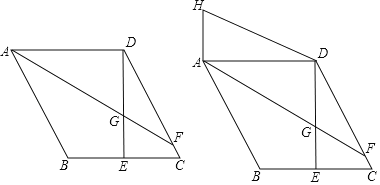
【题目】如图,在平行四边形ABCD中,过点D作DE⊥BC交BC于点E,且DE=AD,F为DC上一点,且AD=FD,连接AF与DE交于点G.
(1)若∠C=60°,AB=2,求GF的长;
(2)过点A作AH⊥AD,且AH=CE,求证:AB=DG+AH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极推行“互动生成的学本课堂”卓有成效,“小组合作学习”深入人心,九年级某学习小组在操作实践过程中发现了一个有趣的问题:将直尺和三角板(三角板足够大)按如图所示的方式摆放在平面直角坐标系中,直尺的左侧边CD在直线x=4上,在保证直角三角板其中一条直角边始终过点A(0,4),同时使得直角顶点E在CD上滑动,三角板的另一直角边与x轴交于点B,当点E从点C(4,5)滑动到点D(4,0)的过程中,点B所经过的路径长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com