
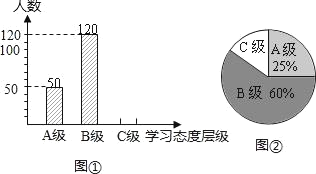
【题目】2011年,陕西西安被教育部列为“减负”工作改革试点地区.学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
科目:初中数学 来源: 题型:
【题目】某校为了了解了解节能减排、垃圾分类等知识的普及情况,从该校2000名学生中随机抽取了部分学生进行调查调查,调查结果分为“非常了解“、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制出以下两幅不完整的统计图,请根据统计图回答下列问题:
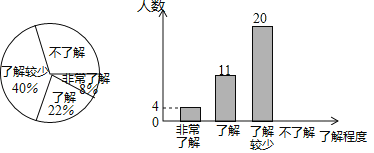
(1)本次调查的学生共有 人,估计该校2000名学生中“不了解”的人数约有 人.
(2)“非常了解”的4人中有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图和列表的方法,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )

A. 4 B. 6 C. 8 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
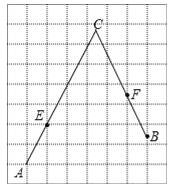
【题目】如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.
(Ⅰ)AE的长等于 ;
(Ⅱ)若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
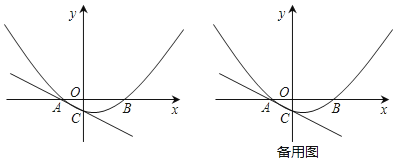
【题目】如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣![]() x﹣1交于点C.
x﹣1交于点C.
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;
(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
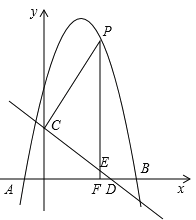
【题目】如图,抛物线![]() 与
与![]() 轴交于A (-1,0),B (5,0)两点,直线
轴交于A (-1,0),B (5,0)两点,直线![]() 与y轴交于点
与y轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是x轴上方的抛物线上一动点,过点
是x轴上方的抛物线上一动点,过点![]() 作
作![]() ⊥
⊥![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点,是否存在点
的对称点,是否存在点![]() ,使点
,使点![]() 落在
落在![]() 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
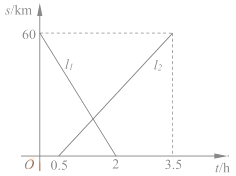
【题目】A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
(1)表示乙离开A地的距离与时间关系的图像是________(填![]() );
);
甲的速度是__________km/h;乙的速度是________km/h。
(2)甲出发后多少时间两人恰好相距5km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两条射线BA//CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,分别交AB,CD与点A,D.
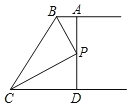
(1)求∠BPC的度数;
(2)若![]() ,求AB+CD的值;
,求AB+CD的值;
(3)若![]() 为a,
为a,![]() 为b,
为b,![]() 为c,求证:a+b=c.
为c,求证:a+b=c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)求证:EG2=![]() GF
GF![]() AF;
AF;
(3)若AB=4,BC=5,求GF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com