
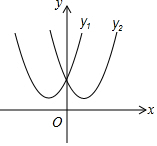
 定义感知:我们把顶点关于y轴对称,且交于y轴上同一点的两条抛物线叫做“孪生抛物线”,如图所示的抛物线y1=x2+2x+2与y2=x2-2x+2是一对“孪生抛物线”.
定义感知:我们把顶点关于y轴对称,且交于y轴上同一点的两条抛物线叫做“孪生抛物线”,如图所示的抛物线y1=x2+2x+2与y2=x2-2x+2是一对“孪生抛物线”.分析 初步运用:(1)①根据“孪生抛物线”的定义即可求解;
②由“孪生抛物线”的意义判断即可;
(2)由“孪生抛物线”的顶点关于y轴对称,所以把解析式化成顶点式,求出其“孪生抛物线”;
延伸拓展:由于MM′=4,“孪生抛物线”与y轴的交点A(0,1)到线段MM′的距离为2个单位长度,可得M(2,-1),M′(-2,-1),或M(2,3),M′(-2,3),其“共点”A与M,M′,O三点恰好构成一个面积为12的菱形,且MM′=4,①开口向上时,求出M(-2,3),M′(2,3),设出“孪生抛物线”把共点A(0,1)代入即可求解.
解答 解:初步运用:
(1)①∵把顶点关于y轴对称,且交于y轴上同一点的两条抛物线叫做“孪生抛物线”,
∴“孪生抛物线”的两对称轴一定关于y轴对称;
②“孪生抛物线”的开口方向一定相同,原来的说法是错误的.
(2)∵抛物线y=2x2-4x-1=2(x-1)2-3,
∴它的“孪生抛物线”为y=2(x+1)2-3=2x2+4x-1,
延伸拓展:∵MM′=4,
∴M(2,y),M′(-2,y),
∵“孪生抛物线”与y轴的交点A(0,1)到线段MM′的距离为2个单位长度,
∴M(2,-1),M′(-2,-1),或M(2,3),M′(-2,3),
∴由此可设“孪生抛物线”的解析式为:y=a(x+2)2-1与y=a(x-2)2-1,
∵点A(0,1)在“孪生抛物线”的图象上,
∴1=a×22-1,
∴a=$\frac{1}{2}$,
∴“孪生抛物线”的解析式为:y=$\frac{1}{2}$(x+2)2-1与y=$\frac{1}{2}$(x-2)2-1;
由此可设“孪生抛物线”的解析式为:y=a(x+2)2-3与y=a(x-2)2-3,
∵点A(0,1)在“孪生抛物线”的图象上,
∴1=a×22-3,
∴a=1,
∴“孪生抛物线”的解析式为:y=(x+2)2-3与y=(x-2)2-3.
故答案为:√;×;y=2x2+4x-1.
点评 此题是二次函数综合题,主要考查了新定义的理解和掌握,二次函数的性质,解决二次函数的方法一样,解本题的关键是掌握“孪生抛物线”的定义.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:填空题
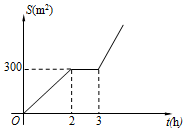 某社区有一块空地需要绿化,某绿化组承担了此项任务,该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示.3小时后,绿化组每小时比开始多完成50m2,则当t>3时,S与t的函数关系式为S=200t-300.
某社区有一块空地需要绿化,某绿化组承担了此项任务,该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示.3小时后,绿化组每小时比开始多完成50m2,则当t>3时,S与t的函数关系式为S=200t-300.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
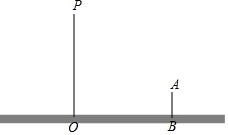 晚上,小亮在广场乘凉,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯
晚上,小亮在广场乘凉,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com