
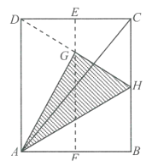
【题目】如图,在一张矩形纸片![]() 中,对角线
中,对角线![]() ,点
,点![]() 分别是
分别是![]() 和
和![]() 的中点,现将这张纸片折叠,使点
的中点,现将这张纸片折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,若
,若![]() 的延长线恰好经过点
的延长线恰好经过点![]() ,则点
,则点![]() 到对角线
到对角线![]() 的距离为( )
的距离为( )![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
设DH与AC交于点M,易得EG为△CDH的中位线,所以DG=HG,然后证明△ADG≌△AHG,可得AD=AH,∠DAG=∠HAG,可推出∠BAH=∠HAG=∠DAG=30°,然后设BH=a,则BC=AD=AH=2a,利用勾股定理建立方程可求出a,然后在Rt△AGM中,求出GM,AG,再求斜边AM上的高即为G到AC的距离.
如图,设DH与AC交于点M,过G作GN⊥AC于N,

∵E、F分别是CD和AB的中点,
∴EF∥BC
∴EG为△CDH的中位线
∴DG=HG
由折叠的性质可知∠AGH=∠B=90°
∴∠AGD=∠AGH=90°
在△ADG和△AHG中,
∵DG=HG,∠AGD=∠AGH,AG=AG
∴△ADG≌△AHG(SAS)
∴AD=AH,AG=AB,∠DAG=∠HAG
由折叠的性质可知∠HAG=∠BAH,
∴∠BAH=∠HAG=∠DAG=![]() ∠BAD=30°
∠BAD=30°
设BH=a,
在Rt△ABH中,∠BAH=30°
∴AH=2a
∴BC=AD=AH=2a,AB=![]()
在Rt△ABC中,AB2+BC2=AC2
即![]()
解得![]()
∴DH=2GH=2BH=![]() ,AG=AB=
,AG=AB=![]()
∵CH∥AD
∴△CHM∽△ADM
∴![]()
∴AM=![]() AC=
AC=![]() ,HM=
,HM=![]() DH=
DH=![]()
∴GM=GH-HM=![]()
在Rt△AGM中,![]()
∴![]()
故选B.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,AC=BC= ![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B.
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B.
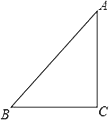
(1)请你在图中把图补画完整;
(2)求C′B的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(![]() , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
查看答案和解析>>
科目:初中数学 来源: 题型:
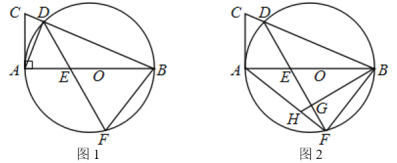
【题目】如图1,AB为⊙O的直径,AC与⊙O相切于点A,BC与⊙O交于点D,点F是直径AB下方半圆上一点(不与A,B重合),连接DF,交AB于点E,
(1)求证:∠C=∠F;
(2)如图2,若DF=DB,连接AF.
①求证:∠FAE=2∠AFE;
②作BH⊥FD于点G,与AF交于点H.若AH=2HF,CD=1,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师提出问题:如图1,有一张长![]() ,宽
,宽![]()
![]() 的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成-一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大.下 面是探究过程,请补充完整:
的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成-一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大.下 面是探究过程,请补充完整:
(1)设小正方形的边长为![]() ,体积为
,体积为![]() ,根据长方体的体积公式得到
,根据长方体的体积公式得到![]() 和
和![]() 的关系式 ;
的关系式 ;
(2)确定自变量![]() 的取值范围是
的取值范围是
(3)列出![]() 与
与![]() 的几组对应值.
的几组对应值.

| ··· |
|
|
|
|
|
|
|
|
|
|
| ··· |
|
|
|
|
|
|
|
|
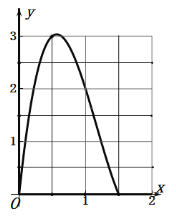
(4)在平面直角坐标系![]() 中,描出以补全后的表中各对对应值为坐标的点画出该函数的图象如图2,结合画出的函数图象,当小正方形的边长约为
中,描出以补全后的表中各对对应值为坐标的点画出该函数的图象如图2,结合画出的函数图象,当小正方形的边长约为 ![]() 时, 盒子的体积最大,最大值约为
时, 盒子的体积最大,最大值约为![]() .(估读值时精确到
.(估读值时精确到![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料
材料1:若一个自然数,从左到右各位数上的数字与从右到左各位数上的数字对应相同,则称为“对称数”.
材料2:对于一个三位自然数![]() ,将它各个数位上的数字分别2倍后取个位数字,得到三个新的数字
,将它各个数位上的数字分别2倍后取个位数字,得到三个新的数字![]() ,
,![]() ,
,![]() ,我们对自然数
,我们对自然数![]() 规定一个运算:
规定一个运算:![]() .
.
例如:![]() 是一个三位的“对称数”,其各个数位上的数字分别2倍后取个位数字分别是:2、8、2.
是一个三位的“对称数”,其各个数位上的数字分别2倍后取个位数字分别是:2、8、2.
则![]() .
.
请解答:
(1)一个三位的“对称数”![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的所有值,
的所有值,![]() ;
;
(2)已知两个三位“对称数”![]() ,若
,若![]() 能被11整数,求
能被11整数,求![]() 的所有值.
的所有值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是( )
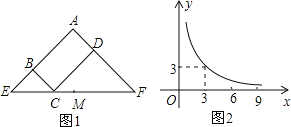
A.当x=3时,EC<EM
B.当y=9时,EC>EM
C.当x增大时,BEDF的值增大
D.当x变化时,四边形BCDA的面积不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O的直径AB与弦CD相交于点E,且E为CD中点,过点B作CD的平行线交弦AD的延长线于点F .
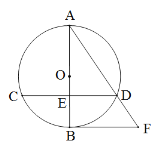
(1)求证:BF是⊙O的切线;
(2)连结BC,若⊙O的半径为2,tan∠BCD=![]() ,求线段AD的长.
,求线段AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com