
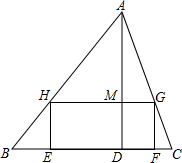 如图所示,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.
如图所示,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M. ×160×120=
×160×120= y(120-x)+
y(120-x)+ x(y+160),
x(y+160), x+160;
x+160; x+160代入S=xy,
x+160代入S=xy, x2+160x;
x2+160x; x2+160x,
x2+160x, (x-60)2+4800;
(x-60)2+4800; (x-60)2≤0,
(x-60)2≤0, (x-60)2=0时,即x=60时,S=-
(x-60)2=0时,即x=60时,S=- (x-60)2+4800有最大值4800.
(x-60)2+4800有最大值4800. ×160×120=
×160×120= y(120-x)+
y(120-x)+ x(y+160),继而求得答案;
x(y+160),继而求得答案; x+160代入S=xy,即可求得S与x的函数关系式;
x+160代入S=xy,即可求得S与x的函数关系式; x2+160x,可得:S=-
x2+160x,可得:S=- (x-60)2+4800;则可求得矩形EFGH的面积S最大值.
(x-60)2+4800;则可求得矩形EFGH的面积S最大值.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
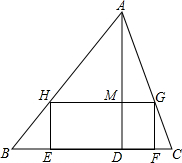 如图所示,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.
如图所示,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.查看答案和解析>>
科目:初中数学 来源: 题型:
 在底边长BC=20cm,高AM=12cm的三角形铁板ABC上,要截一块矩形铁板EFGH,如图所示,当矩形的边EF=
在底边长BC=20cm,高AM=12cm的三角形铁板ABC上,要截一块矩形铁板EFGH,如图所示,当矩形的边EF=查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
 所在圆的圆心O(
所在圆的圆心O( 保留作图痕迹,不写作法);
保留作图痕迹,不写作法); 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com