
【题目】已知正方形![]() 的边长为4,点
的边长为4,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,当![]() 时,求证:
时,求证:![]() 平分
平分![]() ;
;
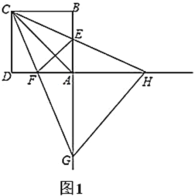
(2)如图2,将图1中的![]() 绕点
绕点![]() 逆时针旋转,其他条件不变,(1)的结论是否成立?说明理由;
逆时针旋转,其他条件不变,(1)的结论是否成立?说明理由;
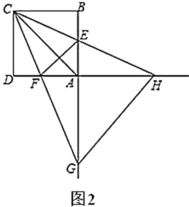
(3)当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的长.
的长.
【答案】(1)证明见解析;(2)成立,理由见解析;(3)AG的长为4或![]() 或8
或8
【解析】
(1)先证![]() CDF≌
CDF≌![]() CBE,进而可得
CBE,进而可得![]() ,CF=CE,由此可得∠DFC=67.5°,再根据
,CF=CE,由此可得∠DFC=67.5°,再根据![]() ,CF=CE可求得
,CF=CE可求得![]() ,进而可证得FC平分∠DFE;
,进而可证得FC平分∠DFE;
(2)延长AD到M,使DM=BE,先证![]() DMC≌
DMC≌![]() BEC,可得CM=CE,∠MCD=∠ECB,再证
BEC,可得CM=CE,∠MCD=∠ECB,再证![]() MCF≌
MCF≌![]() ECF,由此可得∠MFC=∠EFC,进而可证得FC平分∠DFE;
ECF,由此可得∠MFC=∠EFC,进而可证得FC平分∠DFE;
(3)分三种情形画出图形分别求解即可解决问题.
(1)证明:∵四边形ABCD是正方形,
∴CD=CA,∠B=∠D=∠DCA=90°
又DF=BE,
∴![]() CDF≌
CDF≌![]() CBE(SAS)
CBE(SAS)
∴![]() ,CF=CE,
,CF=CE,
∴∠DFC=90°-22.5°=67.5°,![]() ,
,
∴∠DFC=∠CFE,
∴FC平分∠DFE;
(2)解:成立,
延长AD到M,使DM=BE,
∵四边形ABCD是正方形,
∴CB=CD,∠CDA=∠B=∠DCB=90°,
∴∠DCF+∠ECB=90°-∠ECF=45°,
∵∠CDM=180°-∠CDA=90°=∠B
∴![]() DMC≌
DMC≌![]() BEC(SAS)
BEC(SAS)
∴CM=CE,∠MCD=∠ECB,
∴∠DCF+∠MCD=45°,
即∠MCE=∠ECF=45°,
又CF=CF,
∴![]() MCF≌
MCF≌![]() ECF(SAS),
ECF(SAS),
∴∠MFC=∠EFC,
∴FC平分∠DFE,
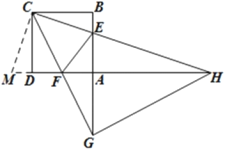
(3)解:如图1,当GC=GH时,
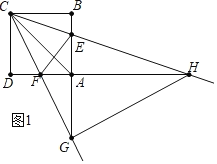
∵∠GCH=45°,
∴∠GHC=∠GCH=45°,
∴∠CGH=90°,
∴∠CGB+∠AGH=90°,
∵∠B=90°,
∴∠CGB+∠BCG=90°,
∴∠AGH=∠BCG,
∴![]() AHG≌
AHG≌![]() BGC(AAS),
BGC(AAS),
∴AG=BC=4;
如图2,当CH=HG时,
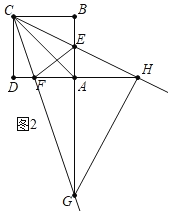
同理可以证明![]() GAH≌
GAH≌![]() HDC
HDC
∴AH=BC=4,
∴AG=DH=AD+AH=8.
如图3,当CG=CH时,
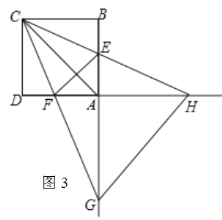
则∠CGH=∠CHG=![]() (180°﹣45°)=67.5°.
(180°﹣45°)=67.5°.
∵∠B=∠D=90°,CD=CB,CH=CG,
∴Rt![]() CDH≌Rt
CDH≌Rt![]() CBG(HL)
CBG(HL)
∴DH=BG,
又∵AD=AB,
∴AH=AG,
∴∠AGH=∠AHG=45°,
∴∠AGC=∠CGH﹣∠AGH=22.5°,
∵CG=CH,AC=AC,AG=AH,
∴![]() DMC≌
DMC≌![]() BEC(SSS),
BEC(SSS),
∴∠ACG=∠ACH=22.5°,
∴∠ACG=∠AGC,
∴AC=AG,
∵在Rt![]() ACD中,AC=
ACD中,AC=![]() ,
,
∴AG=![]() ,
,
综上所述,AG的长为4或![]() 或8.
或8.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】某水果店3月份购进甲种水果50千克、乙种水果80千克,共花费1700元,其中甲种水果以15元/千克,乙种水果以20元/千克全部售出;4月份又以同样的价格购进甲种水果60千克、乙种水果40千克,共花费1200元,由于市场不景气,4月份两种水果均以3月份售价的8折全部售出.
(1)求甲、乙两种水果的进价每千克分别是多少元?
(2)请计算该水果店3月和4月甲、乙两种水果总赢利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线G:![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点;一次函数
与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点;一次函数![]() (
(![]() )的图像为直线
)的图像为直线![]() .
.
(1)求A、B两点的坐标;
(2)当1≤x≤2时,![]() ≤
≤![]() ≤
≤![]() ,试说明:抛物线G的顶点不在直线
,试说明:抛物线G的顶点不在直线![]() 上;
上;
(3)设![]() ,直线
,直线![]() 与线段AC交于D点,与y轴交于E点,与抛物线G的对称轴交于F 点,当A、C两点到直线
与线段AC交于D点,与y轴交于E点,与抛物线G的对称轴交于F 点,当A、C两点到直线![]() 距离相等时,是否存在整数n,使F点在直线BE的上方?若存在,求n的值;若不存在,请说明理由.
距离相等时,是否存在整数n,使F点在直线BE的上方?若存在,求n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,现有甲、乙、丙三辆汽车经过这个路口.
(1)求甲、乙两辆汽车向同一方向行驶的概率;
(2)甲、乙、丙三辆汽车向同一方向行驶的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
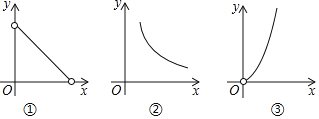
【题目】在如图所示的三个函数图象中,有两个函数图象能近似地刻画如下a,b两个数学问题:
问题a:矩形面积为4,它的长y与宽x之间的函数关系;
问题b:矩形周长为8,它的长y与宽x之间的函数关系.
(1)问题a,b所对应的函数图象分别为 ,(填写序号);
(2)请你把剩下的函数图象写出一个适合的数学问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,点
上,点![]() 为弦
为弦![]() 的中点,射线
的中点,射线![]() 与圆周及切线
与圆周及切线![]() 分别交于点
分别交于点![]() 和点
和点![]() ,连接
,连接![]() .
.
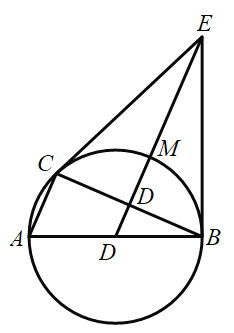
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)若直径![]() ,填空:①连接
,填空:①连接![]() ,当
,当![]() _________
_________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]() ________时,四边形
________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为 1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为( )
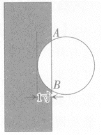
A.13B.24C.26D.28
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com