
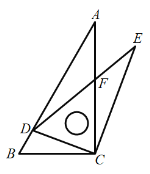
【题目】如图,两个大小不同的三角板放在同一平面内,直角顶点重合于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() _________.
_________.
【答案】![]()
【解析】
过点C作CM⊥DE于点M,先证![]() BCD∽
BCD∽![]() ACE,求出AE的长及∠CAE=60°,推出∠DAE=90°,在Rt
ACE,求出AE的长及∠CAE=60°,推出∠DAE=90°,在Rt![]() DAE中利用勾股定理求出DE的长,进一步求出CE的长,再证
DAE中利用勾股定理求出DE的长,进一步求出CE的长,再证![]() AFD∽
AFD∽![]() EFC,利用相似三角形对应边的比相等即可求出
EFC,利用相似三角形对应边的比相等即可求出![]() 的比值.
的比值.
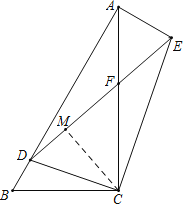
解:如图,过点C作CM⊥DE于点M,
∵BD=2,AD=8,
∴AB=BD+AD=10,
∵在Rt△ABC中,∠BAC=30°,∠B=90°﹣∠BAC=60°,
∴BC=![]() AB=5,AC=
AB=5,AC=![]() BC=5
BC=5![]() ,
,
在Rt![]() BCA与Rt
BCA与Rt![]() DCE中,
DCE中,
∵∠BAC=∠DEC=30°,
∴tan∠BAC=tan∠DEC,
∴![]() ,
,
∵∠BCA=∠DCE=90°,
∴∠BCA﹣∠DCA=∠DCE﹣∠DCA,
∴∠BCD=∠ACE,
∴![]() BCD∽
BCD∽![]() ACE,
ACE,
∴∠CAE=∠B=60°,![]() ,
,
∴∠DAE=∠DAC+∠CAE=30°+60°=90°,![]() ,
,
∴AE=2![]() ,
,
在Rt![]() ADE中,DE=
ADE中,DE=![]() =
=![]() ,
,
在Rt![]() DCE中,∠DEC=30°,
DCE中,∠DEC=30°,
∴∠EDC=60°,CE=![]() DE=
DE=![]() ,
,
∵∠BAC=∠CEF,∠AFD=∠EFC,
∴![]() AFD∽
AFD∽![]() EFC,
EFC,
∴![]() ,
,
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图(1),已知点![]() 在正方形
在正方形![]() 的对角线
的对角线![]() 上,
上,![]() 垂足为点
垂足为点![]() ,垂足为点
,垂足为点![]() .
.
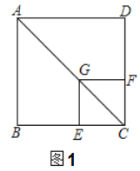
(1)证明与推断:
![]() 求证:四边形
求证:四边形![]() 是正方形;
是正方形;
![]() 推断:
推断:![]() 的值为_ _;
的值为_ _;
(2)探究与证明:
将正方形![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 角
角![]() ,如图(2)所示,试探究线段
,如图(2)所示,试探究线段![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)拓展与运用:
若![]() ,正方形
,正方形![]() 在绕点
在绕点![]() 旋转过程中,当
旋转过程中,当![]() 三点在一条直线上时,则
三点在一条直线上时,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
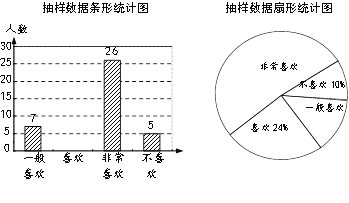
【题目】某校用随机抽样的方法在九年级开展了“你是否喜欢网课”的调查,并将得到的数据整理成了以下统计图(不完整).
(1)此次共调查了 名学生;
(2)请将条形统计图补充完整;
(3)若该学校九年级共有300名学生,请你估计其中“非常喜欢”网课的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市“青山绿水”行动中,某社区计划对面积为![]() 的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为
的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为![]() 区域的绿化时,甲队比乙队少用6天.
区域的绿化时,甲队比乙队少用6天.
(1)求甲、乙两工程队每天各能完成多少面积的绿化;
(2)若甲队每天绿化费用是1.2万元,乙队每天绿化费用为0.5万元,社区要使这次绿化的总费用不超过40万元,则至少应安排乙工程队绿化多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
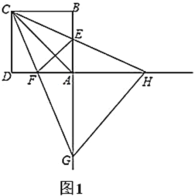
【题目】已知正方形![]() 的边长为4,点
的边长为4,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,当![]() 时,求证:
时,求证:![]() 平分
平分![]() ;
;
(2)如图2,将图1中的![]() 绕点
绕点![]() 逆时针旋转,其他条件不变,(1)的结论是否成立?说明理由;
逆时针旋转,其他条件不变,(1)的结论是否成立?说明理由;
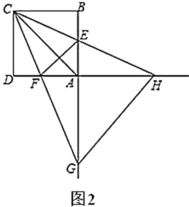
(3)当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量建筑物CD、EF的高度,在直线CE上选取观测点A、B,AC的距离为40米.从A、B测得建筑物的顶部D的仰角分别为51.34°、68.20°,从B、D测得建筑物的顶部F的仰角分别为64.43°、26.57°.
(1)求建筑物CD的高度;
(2)求建筑物EF的高度.
(参考数据:tan51.34°≈1.25,tan68.20°≈2.5,tan64.43°≈2,tan26.57°≈0.5)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网络销售是一种重要的销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克10元.公司在试销售期间,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中![]() ).
).
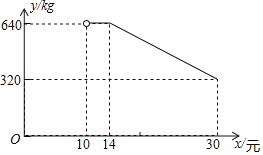
(1)直接写出y与x之间的函数关系式及自变量的取值范围.
(2)若农贸公司每天销售该特产的利润要达到3100元,则销售单价x应定为多少元?
(3)设每天销售该特产的利润为W元,若![]() ,求:销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
,求:销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
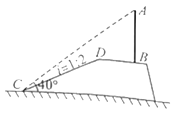
【题目】为积极宣传国家相关政策,某村在一山坡的顶端的平地上竖立一块宣传牌![]() .小明为测得宣传牌的高度,他站在山脚
.小明为测得宣传牌的高度,他站在山脚![]() 处测得宣传牌的顶端
处测得宣传牌的顶端![]() 的仰角为
的仰角为![]() ,已知山坡
,已知山坡![]() 的坡度
的坡度![]() ,山坡
,山坡![]() 的长度为
的长度为![]() 米,山坡顶端
米,山坡顶端![]() 与宣传牌底端
与宣传牌底端![]() 的水平距离为2米,求宣传牌的高度
的水平距离为2米,求宣传牌的高度![]() (精确到1米)
(精确到1米)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com